Предмет: Алгебра,
автор: alexanderoginskiy
Решите систему уравнений
Приложения:
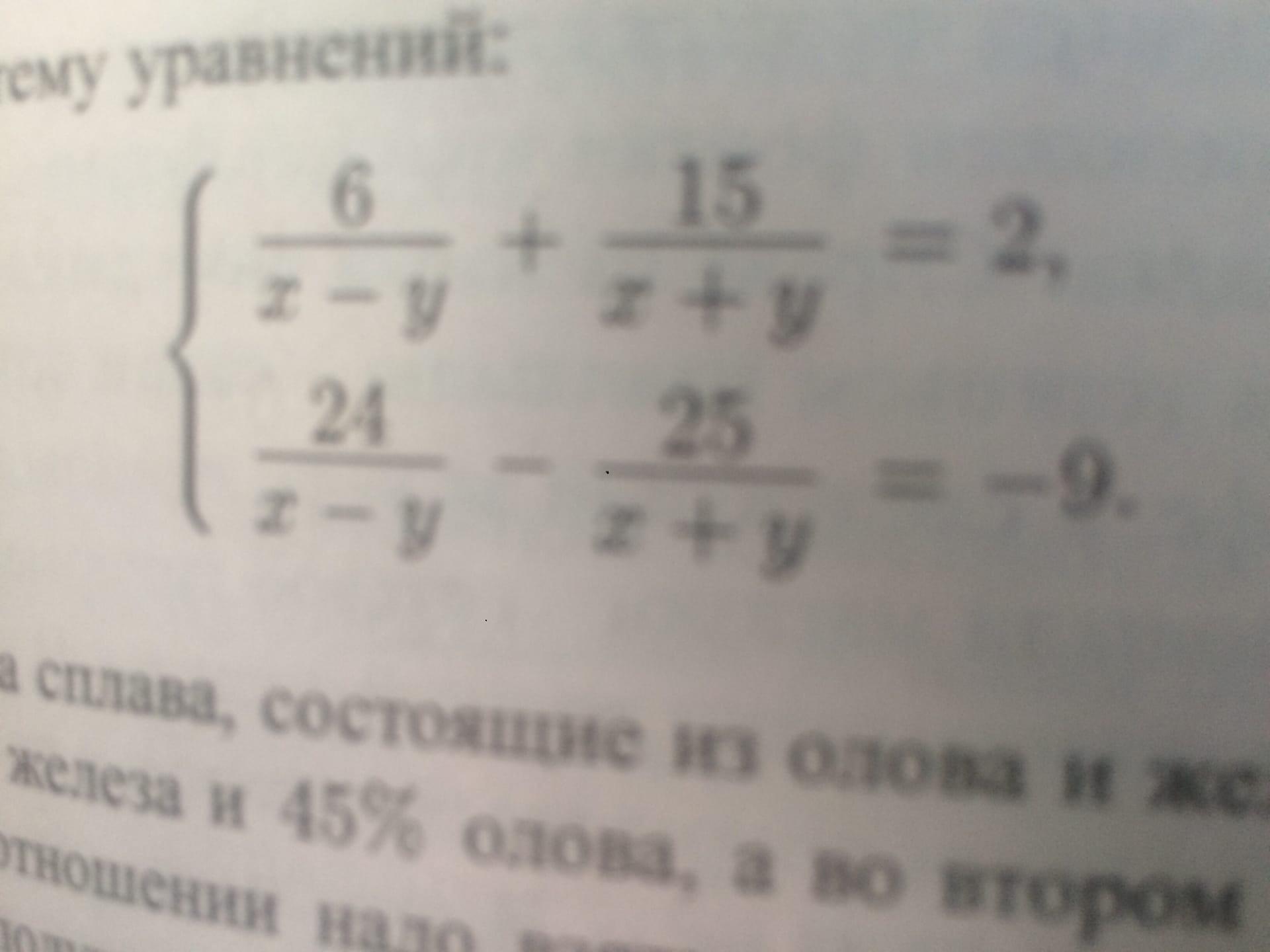
alexanderoginskiy:
методом подстановки
Ответы
Автор ответа:
0
1) Упростить систему уравнений при помощи замены переменных:
2) Решить систему уравнений, используя метод замены переменных:
3) Выполнить обратную замену:
4) Решить систему уравнений, используя метод исключения переменных:
Автор ответа:
0
1) Замена:
ОДЗ:
2) Решаем новую систему уравнений:
Сложим:
Подставим в первое и найдем :
3) Обратная замена:
ОДЗ:
Сложим:
Ответ: (-0,5; 5,5)
Похожие вопросы
Предмет: Математика,
автор: mylanalysenko
Предмет: Математика,
автор: Ffgggdhdhhfbdbd
Предмет: Английский язык,
автор: lana0504star
Предмет: Обществознание,
автор: Этпростя