Question

На сторонах АВ, ВС, СА треугольника АВС выбраны точки Р, Q и R соответственно так, что ВQ — ВР и АР — AR. Оказалось, биссектриса угла ВQR. Hайдите угол ARP, eсли угол QRC равен 69°. Ответ дайте в градусах.​

Answer 1

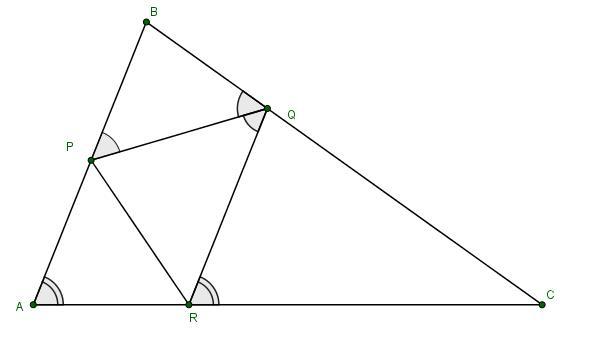
Задача. На сторонах АВ, ВС, СА треугольника АВС выбраны точки Р, Q и R соответственно так, что ВQ = ВР и АР = AR. Оказалось, PQ биссектриса угла ВQR. Hайдите угол ARP, eсли угол QRC равен 69°. Ответ дайте в градусах.​

               Решение:

Пусть $\angle BQR=2\alpha$, тогда поскольку PQ - биссектриса, то $\angle BQP=\angle PQR=\alpha$, но по условию, PB = BQ ⇒ ΔBPQ - равнобедренный, следовательно, $\angle BPQ=\alpha$, но так как $\angle BPQ=\angle PQR$ - накрест лежащие углы равны, то $AB \parallel QR$ (первый признак параллельности прямых).

$\angle CRQ=\angle CAB$ как соответственные углы при AB || QR и секущей CA.

Аналогично, по условию AP = AR ⇒ ΔAPR - равнобедренный, следовательно, $\angle ARP=\dfrac{180^\circ-\angle PAR}{2}=\dfrac{180^\circ-69^\circ}{2}=55{,}5^\circ$

Ответ: $55{,}5^\circ.$