Question

СРОЧНО!!! Помогите
1)В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС. Докажите, что треугольники BEF и DFE равны.

Найдите площадь параллелограмма DEBF, если FE = 6, a DF = 3.
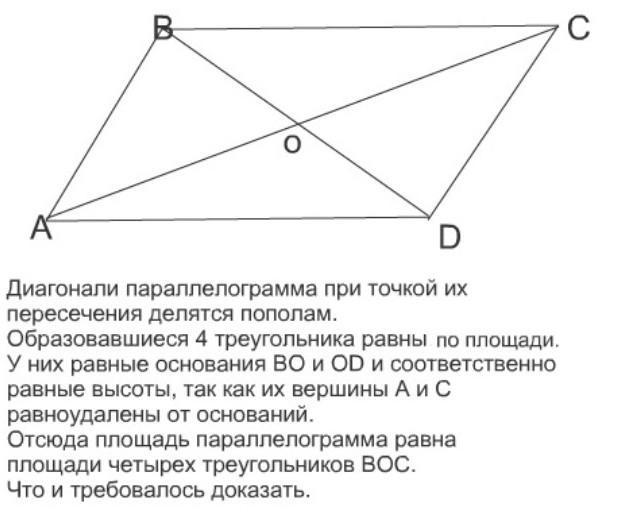
2)В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.

Найдите площадь параллелограмма ABCD, если площадь треугольника ВСО равна 3.

​

Answer 1

1) ∆ ABE = ∆ CDF (AB = DC - т.к ABCD параллелограмм, BE=DF - высоты в равных треугольниках АВС и ADC) ⇒ AE = CF

∆BFC = ∆DEA (по двум сторонам и углу между ними) ⇒ BF = ED

2) на фотке