Question

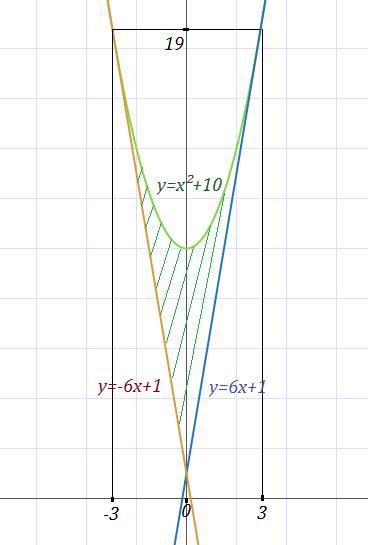
Найти площадь фигуры ограниченной линиями У=х^2+10 (парабола) и касательными к этой параболе проведенной из точки с координатами 0;1

Answer 1

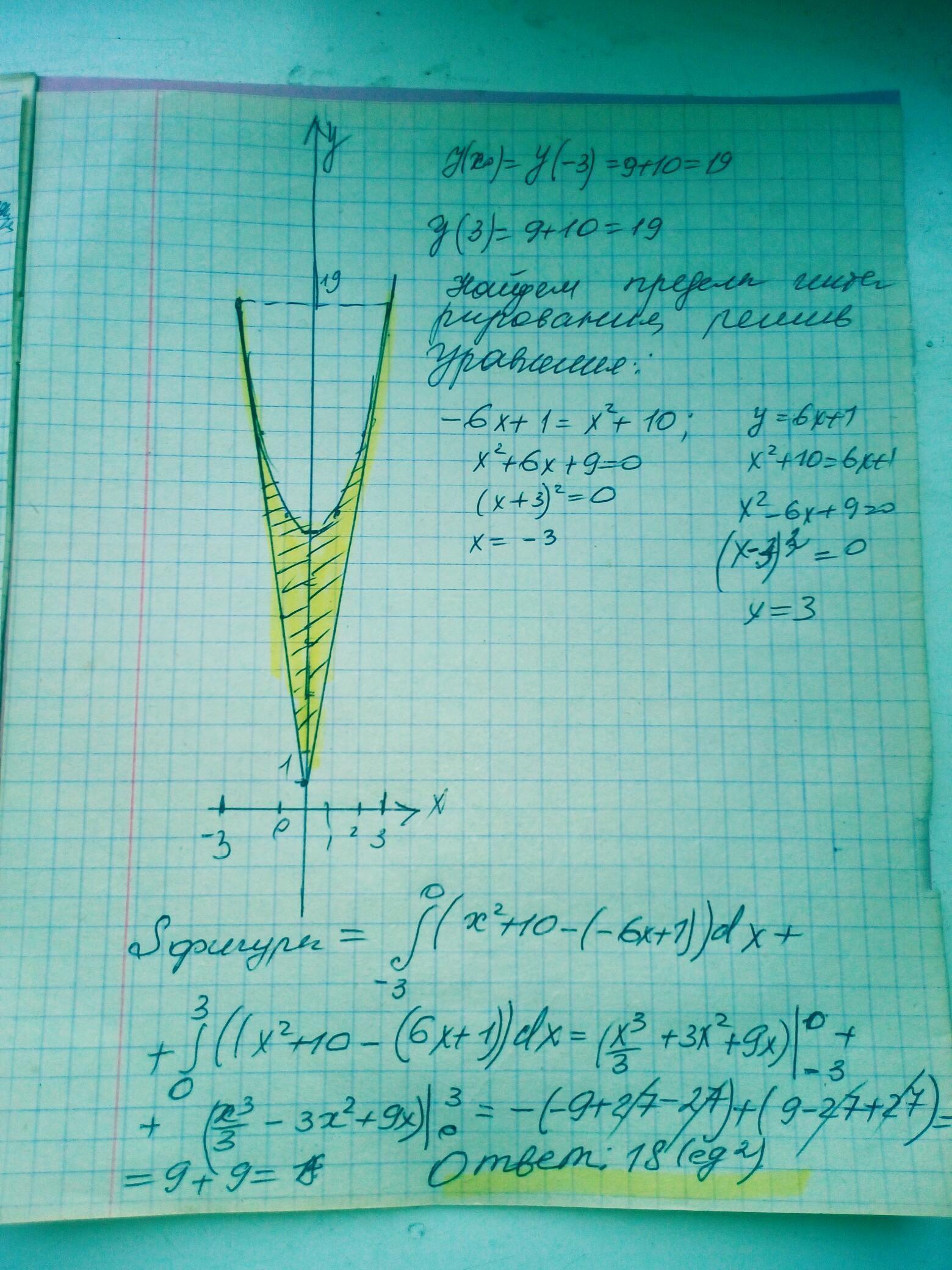
Ответ:   S=18 кв.ед.

Пошаговое объяснение:

$y=x^2+10$

Составим уравнения касательных:  $y=y(x_0)+y'(x_0)\cdot (x-x_0)$ , где  $x_0$ - точка касания .

$y'=2x\; ,\; \; y'(x_0)=2x_0\; \; ,\; \; y(x_0)=x_0^2+10$

Уравнение касательной имеет вид:

$y=(x_0^2+10)+2x_0\cdot (x-x_0)\\\\y=-x_0^2+2x_0\cdot x+10$

Теперь подставим в уравнение касательной координаты точки (0,1), которая принадлежит касательной:

$1=y(0)=-x_0^2+10\; \; \to \; \; x_0^2=9\; \; \; \to \; \; \; x_0=\pm 3$

Получили 2 точки касания х₀=3 и х₀=-3 .

Теперь подставим эти значения в уравнение касательной:

$x_0=3:\; y=-3^2+6x+10\; ,\; \; \underline {y=6x+1}\\\\x_0=-3:\; y=-(-3)^2-6x+10\; ,\; \; \underline {y=-6x+1}$

Получили область между параболой и двумя касательными, симметричную относительно оси ОУ. Поэтому площадь заданной области можно считать как удвоенную площадь области, заключённой между параболой, одной из касательных и оси ОУ.

$S=2\int\limits^3_0\Big ((x^2+10)-(6x+1)\Big ))\, dx=2\int\limits^3_0\, (x-3)^2\, dx=2\cdot \frac{(x-3)^3}{3}\Big |_0^3=\\\\=\frac{2}{3}\cdot (0^3-(-3)^3)=\frac{2\cdot 27}{3}=2\cdot 9=18$

Answer 2

Ответ: во вложении Пошаговое объяснение: