Предмет: Алгебра,
автор: murrrpartner
ПОМОГИТЕ ПОЖАЛУЙСТА!!!
РЕШИТЬ УРАВНЕНИЕ
Приложения:
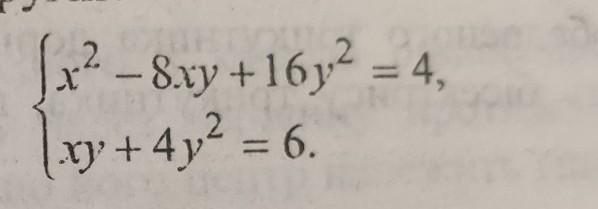
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Физика,
автор: krokodilkolya
Предмет: Математика,
автор: kordunyanuk
Предмет: Геометрия,
автор: ademi1732
Предмет: Алгебра,
автор: selion4200
Предмет: Математика,
автор: ноупроблем