Предмет: Геометрия,
автор: mashakorotchenko123
Найдите площадь трапеции ABCD, если AB=3,BC=5,CD=4,AD=10. ПОЖАЛУЙСТА
Приложения:
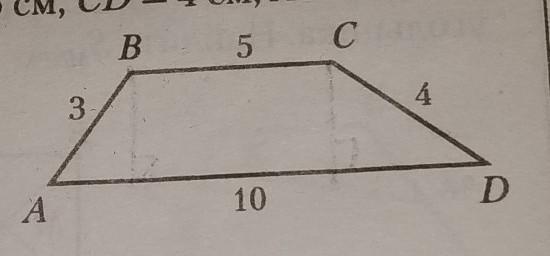
Ответы
Автор ответа:
1
Объяснение:
проведём высоту ВН и СК
теперь НК равно ВС равно (10-5)/2= 2,5 следовательно и АН равно КД, можно найти высоту по теореме Пифагора
ВН²=9- 6,25=2, 75, смотрим какому квадрату равен и потом ищем по формуле аh
Автор ответа:
6
Ответ:
18 см²
Объяснение:
Проведем высоты ВК и СН; ВК=СН.
КН=ВС=5 см
АК+DН=10-5=5 см
Пусть АК=х см, тогда DН=5-х см.
Найдем высоту трапеции по теореме Пифагора:
ВК²=АВ²-АК²=9-х²
СН²=СD²-DН²=16-(5-х)², из этого следует, что
9-х²=16-(25-10х+х²)
9-х²=16-25+10х-х²
9-16+25=10х
10х=18
х=1,8; АК=1,8 см
По теореме Пифагора ВК=√(АВ²-АК²)=√(9-3,24)=√5,76=2,4 см
S(ABCD)=(ВС+АD):2*ВК=(5+10):2*2,4=18 см²
Похожие вопросы
Предмет: Математика,
автор: ermolova0908
Предмет: Геометрия,
автор: cifuamacuno5
Предмет: Английский язык,
автор: kukinggg
Предмет: Геометрия,
автор: Evgeniyversh