Question

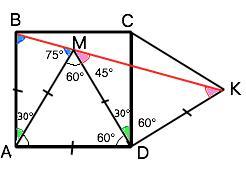
На стороне квадрата ABCD построены равносторонние треугольники - ADM (внутри квадрата) и CDK(вне квадрата). Докажите, что точки B M и K лежат на одной прямой.

Answer 1

   Стороны построенных равносторонних треугольников равны сторонам квадрата.

Углы квадрата равны 90°, углы правильного треугольника 60°.⇒

угол МDС=90°-60°=30°

  Т.к. ∆ СКD  по условию равносторонний, ∠МDС+∠СDК=30°+60°=90°.

  МD=СD=DК ( по условию). ⇒ ∆ МDК - прямоугольный равнобедренный, ⇒ ∠КМD=∠DKM=45°.

  В равнобедренном ∆ ВАМ  ∠ ВАМ=30°,⇒ из суммы углов треугольника углы при основании ВМ содержат по 75°.

 Сумма углов ВМА+АМD+DМК=75°+60°+45°=180°. Следовательно, угол ВМК - развернутый, и точки В, М и К лежат на одной прямой, что и требовалось доказать.