Предмет: Алгебра,
автор: putinnevor
Постройте график и опишите свойства функции
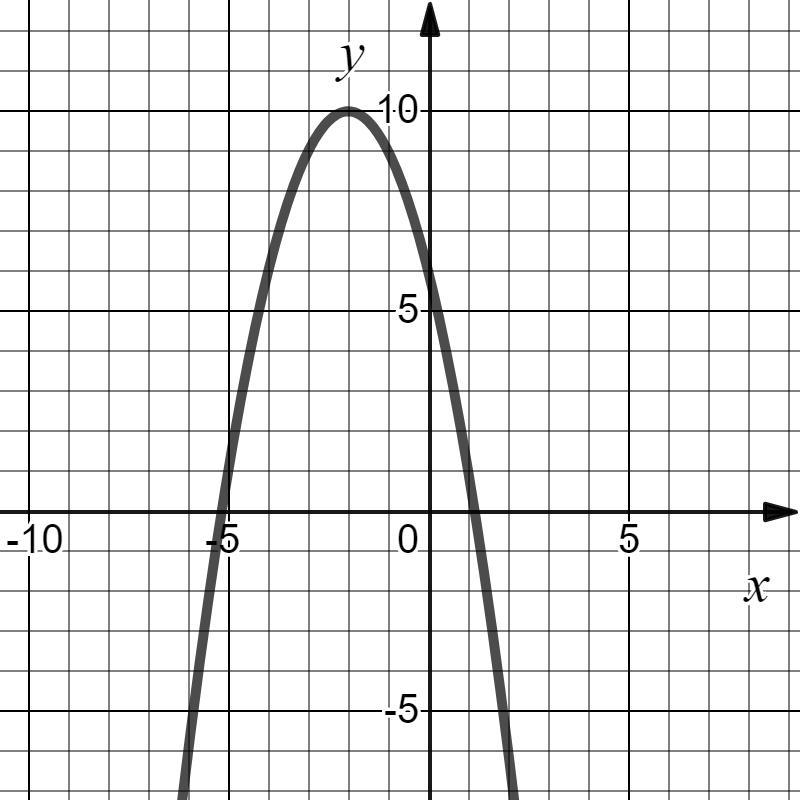
1)f(x)=-x^2-4x+6
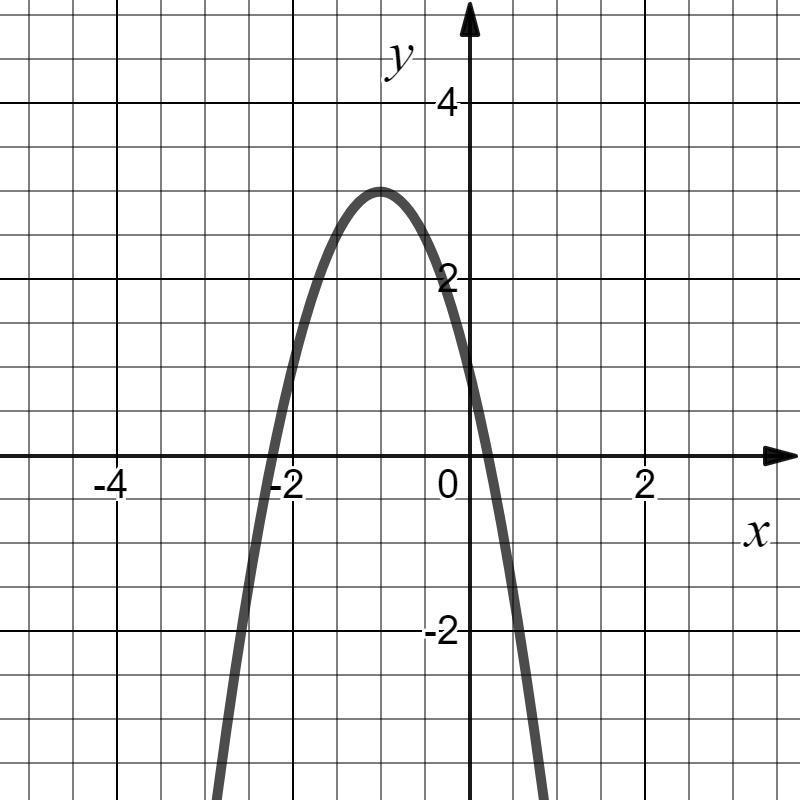
2)f(x)=-2x^2-4x+1
Ответы
Автор ответа:
79
— квадратичная функция, графиком которой является парабола с ветвями, направленными вниз.
- Область определения — ℝ (все действительные числа)
- Точка
— вершина параболы заданной функции
- Область значений —
— функция
ни четная, ни нечетная.
- Функция
возрастает на промежутке
и убывает на промежутке
- Точки пересечения с осями координат:
— с осью ординат: , то есть в точке
— с осью абсцисс:
то есть в точках и
.
— квадратичная функция, графиком которой является парабола с ветвями, направленными вниз.
- Область определения — ℝ (все действительные числа)
- Точка
— вершина параболы заданной функции
- Область значений —
— функция
ни четная, ни нечетная.
- Функция
возрастает на промежутке
и убывает на промежутке
- Точки пересечения с осями координат:
— с осью ординат: , то есть в точке
— с осью абсцисс:
то есть в точках и
.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: nkonstantinova104
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: kiril37chikaluk
Предмет: Математика,
автор: alina5tm
Предмет: Музыка,
автор: mihaa73rus