Предмет: Алгебра,
автор: Meowwwwwwwwwwwwwwwww
ПОМОГИТЕ, ПОЖАЛУЙСТА !! Теория вероятностей
Приложения:
Ответы
Автор ответа:
0
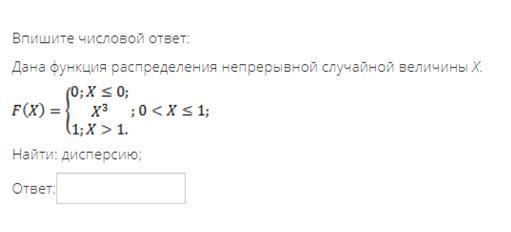
Функция плотности обладает свойством: . Проверим его выполнение, учитывая свойство аддитивности интеграла:
Мы убедились в том, что действительно полученная функция f(х) - плотность непрерывной случайной величины.
Похожие вопросы
Предмет: Английский язык,
автор: hristinasimcuk
Предмет: История,
автор: zafslanalmagambetov1
Предмет: Математика,
автор: gasymovanisa
Предмет: Алгебра,
автор: Alina99999999999
Предмет: Биология,
автор: shashalis