Предмет: Математика,
автор: sanekbikbulatov
Решите уравнение: √√2x²+x-3+2x²-3=x
Приложения:
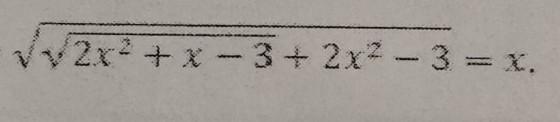
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Подставляя значения, увидим, что решением уравнения является только
Похожие вопросы
Предмет: Алгебра,
автор: gcuk96746
Предмет: Английский язык,
автор: naumova270990
Предмет: Русский язык,
автор: doszhanmaira
Предмет: Литература,
автор: Septilko