Question

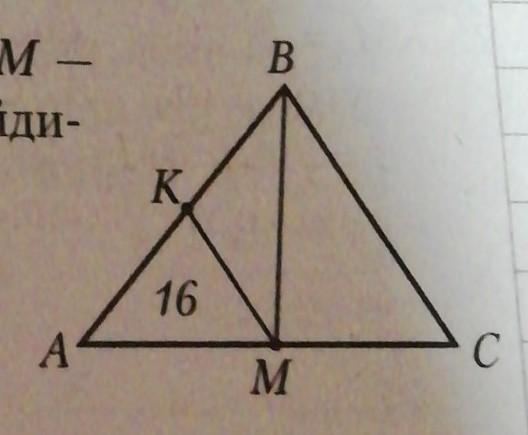
Помогите пожалуйста, В треугольнике ABC (см.рис.) BM - медиана, МК || BC, S(AKM) =16. Найдите S(ABC).​

Answer 1

Ответ:

64

Объяснение:

1. Рассмотрим треугольники AKM и ABC:

• Угол A - общий;
• Угол AKM = углу ABC (как соответственные углы при параллельных прямых KM и BC)

Следовательно, треугольник AKM подобен треугольнику ABC (по двум углам), следовательно, S(abc) : S (akm) = k^2 (коэффициент подобия в квадрате) и AC : AK = k

2. Пусть AM = x, тогда MC = x (т.к. BM - медиана).

AC = AM + MC = x + x = 2x, значит, AC : AK = 2x : x = 2 => k=2

3. S(akm) = 16 (усл)

k = 2

S (abc) : S (akm) = k^2

S(abc) : 16 = 4

S(abc) = 64 - искомая площадь