Question

СРОЧНО!! найдите стороны прямоугольника если известно, что одна из них на 14 см больше дркгой, а диагональ прямоугольника равна 34 см.

Answer 1

Ответ:

30; 30; 16; 16

Объяснение:

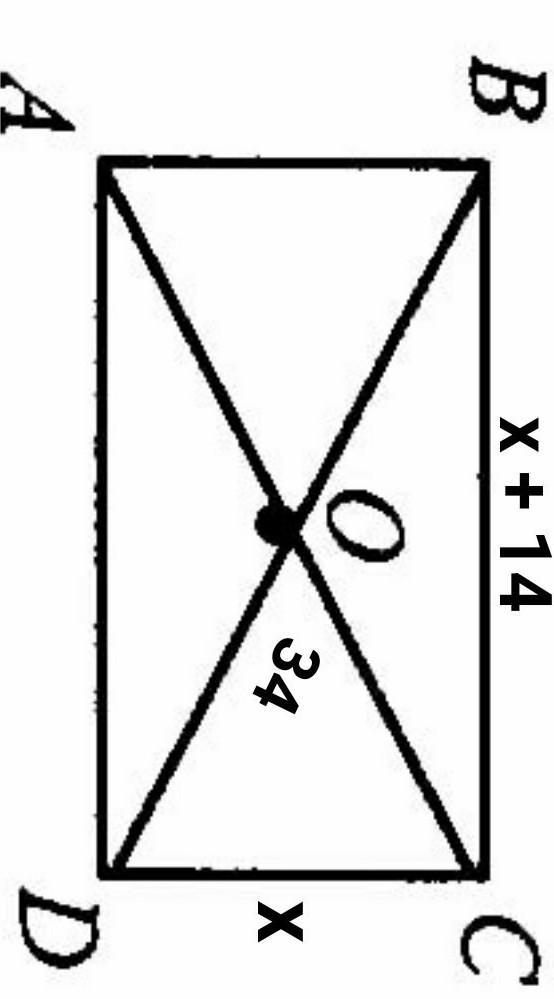
Пусть CD = x, тогда BC = (x + 14). Треугольник BCD - прямоугольный, поэтому решаем по теореме Пифагора. Так как BD = 34, то составим и решим уравнение:

${BD}^{2} = {BC}^{2} + {CD}^{2} \\ {34}^{2} = {(x + 14)}^{2} + {x}^{2} \\ 1156 = {x}^{2} + 28x + 196 + {x}^{2} \\ - {x}^{2} - {x}^{2} - 28x + 196 - 1156 = 0 \\ - 2 {x}^{2} - 28x - 960 = 0 \\ {x}^{2} + 14x + 480 = 0 \\ {x}^{2} + 30x - 16x - 480 = 0 \\ x(x + 30) - 16(x + 30) = 0 \\ (x + 30)(x - 16) = 0 \\ \\ x + 30 = 0 \\ x_{1} = - 30 \\ x - 16 = 0 \\ x_{2} = 16$

x = -30 - не удовлетворяет условию задачи

$x = 16 \: - \: CD$

$x + 14 = 16 + 14 = 30 \: - \: BC$

По свойству прямоугольника:

$BC = AD = 30 \\ AB = CD = 16$