Высота правильной треугольной пирамиды равна 2√3 см, радиус окружности, описанной около ее основания, 4 см.
Найдите: а) апофему пирамиды; б) площадь боковой поверхности пирамиды.
Ответы
Ответ:
а) 4 см.
б) 24√3 см².
Объяснение:
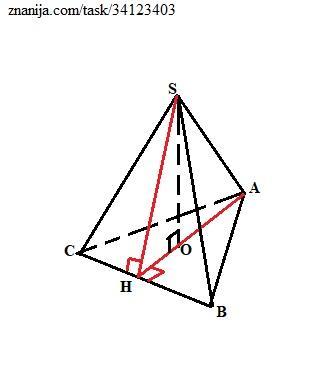
Пирамида SАВС правильная, значит основание - правильный треугольник АВС. Центр О окружности , описанной около ее основания, (правильного треугольника), лежит в центре пересечения высот этого треугольника, являющихся и медианами, и биссектрисами. Следовательно, этот радиус (ОА) равен 2/3 медианы АН (высоты) по свойству медиан. А радиус ОН вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной окружности:
r = ОН =2 см.
Итак, высота треугольника основания равна h = АН = 4·3/2 = 6 см.
Апофема (высота боковой грани) SH составляет с высотой пирамиды SO и радиусом ОН вписанной окружности прямоугольный треугольник SOH в котором по Пифагору найдем эту апофему:
SH = √(SO²+OH²) = √(12+4) = 4 см.
Сторону правильного треугольника можно найти по формуле:
a = (2h√3)/3 = (12√3)/3 = 4√3 см.
Или по Пифагору из треугольника АНВ: АВ² = АН²+HВ².
Зная, что АВ = 2·НВ, получим НВ = 2√3 и
АВ = 2·НВ = 4√3 см.
Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания, то есть
Sбок = SH·3·АВ/2 = 4·3·4√3/2 = 24√3 см².