Предмет: Алгебра,
автор: Аноним
задание номер 133 алгебра
Приложения:
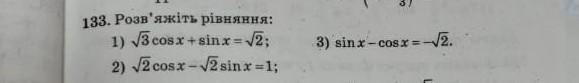
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: kirilnikitin42
Предмет: Қазақ тiлi,
автор: rustamkyzyamina58
Предмет: Українська мова,
автор: popovdaniel22
Предмет: История,
автор: Санс911
Предмет: Литература,
автор: АлинаМороз