Предмет: Геометрия,
автор: mariayaslonimskaya15
Помогите хотя бы рисунок нарисовать, пожалуйста
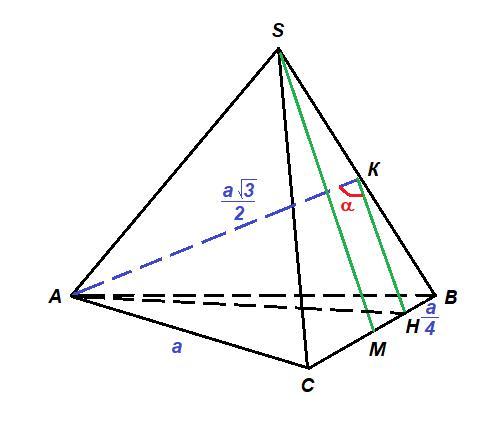
В правильной треугольной пирамиде SABC, боковое ребро которой равно стороне основания, точка K - середина ребра SB, точка M - середина ребра BC. Найдите косинус угла между прямыми AK и SM.
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Прямые АК и SM - скрещивающиеся.
Пусть Н - середина МВ, тогда КН - средняя линия ΔSMB, КН║SM.
∠(АК; SM) = ∠(AK: KH) = ∠AKH = α - искомый угол.
Пусть а - ребро пирамиды (все ребра равны).
как высоты (медианы) равностороннего треугольника.
(средняя линия треугольника SMB)
АН выразим из ΔАВН по теореме косинусов:
∠B = 60°, так как ΔАВС правильный.
Из треугольника АКН по теореме косинусов:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: nkira9406
Предмет: Другие предметы,
автор: 87752567195k
Предмет: Математика,
автор: elenats1810
Предмет: Математика,
автор: fdanil185
Предмет: Математика,
автор: TheVictoriaVin