Нерівності...........
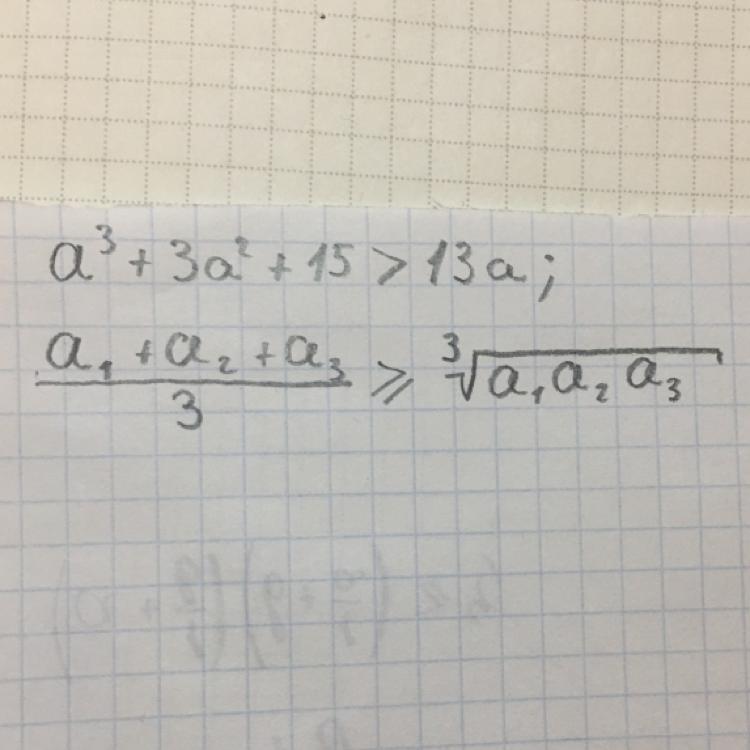
Ответы
Ответ:
В объяснении
Объяснение:
По поводу 2го пункта:
Надо доказать, что
Замена
Последнее неравенство очевидно
Мне кажется , что второе неравенство является указанием к решению первого.
Поэтому я бы решил тут так
Если a> 0 доказать , что
a^3+3*a^2+15>13a
a^3+3*a^2>13*a-15
a^3+3*a^2 +9*a > 22*a- 15
Используя неравенство Коши для 3 степени , что указано ниже :
a^3+3*a^2 +9*a >= 3*∛(27*a^6) =9*a^2
9*a^2> 22*a-15
9*a^2-22*a+15>0
D/4 = 11^2 -9*15 =121- 135<0
Поскольку ветви параболы идут вверх , то
9*a^2-22*a+15>0
a^3+3*a^2 +9*a > 9*a^2>22*a- 15
a^3+3*a^2+15>13a
Что и требовалось доказать
Примечание : заметим , что для a<0 неравенство не всегда выполено.
Контр пример : a=-10
-1000 +300+15>-130
-685>-130 ( что неверно)
Ну и все таки покажу как бы я доказал неравенство Коши для 3 степени .
Сначала докажем для 4 степени используя неравенство для 2 степени
(a1+a2+a3+a4)/4 = ( (a1+a2)/2 +(a3+a4)/2)/2 >= √((a1+a2)/2)*((a3+a4)/2)>=
>= √(√(a1*a2) *√(a3*a4) ) =(a1*a2*a3*a4)^(1/4)
(a1+a2+a3+a4)/4>= (a1*a2*a3*a4)^(1/4)
Пусть : a4= (a1+a2+a3)/3
(a1+a2+a3+a4)/4 = (a1+a2+a3 +(a1+a2+a3)/3 )/4 =(4*(a1+a2+a3)/3)/4= =(a1+a2+a3)/3
(a1+a2+a3)/3 >= (a1*a2*a3*(a1+a2+a3)/3)^1/4
( (a1+a2+a3)/3)^4 >= a1*a2*a3 * (a1+a2+a3)/3
((a1+a2+a3)/3)^3 >= a1*a2*a3
(a1+a2+a3)/3>=∛(a1*a2*a3)
Что и требовалось доказать