Предмет: Математика,
автор: grinfeldmark
Найти точки разрыва функции, если они существуют, скачок функции в каждой
точке разрыва и построить график.
Приложения:
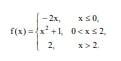
Ответы
Автор ответа:
2
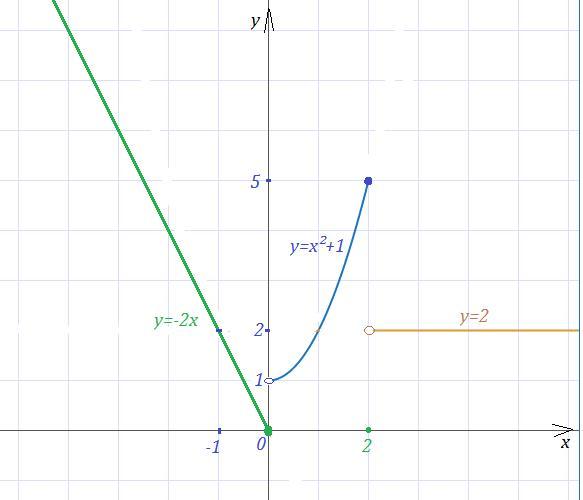
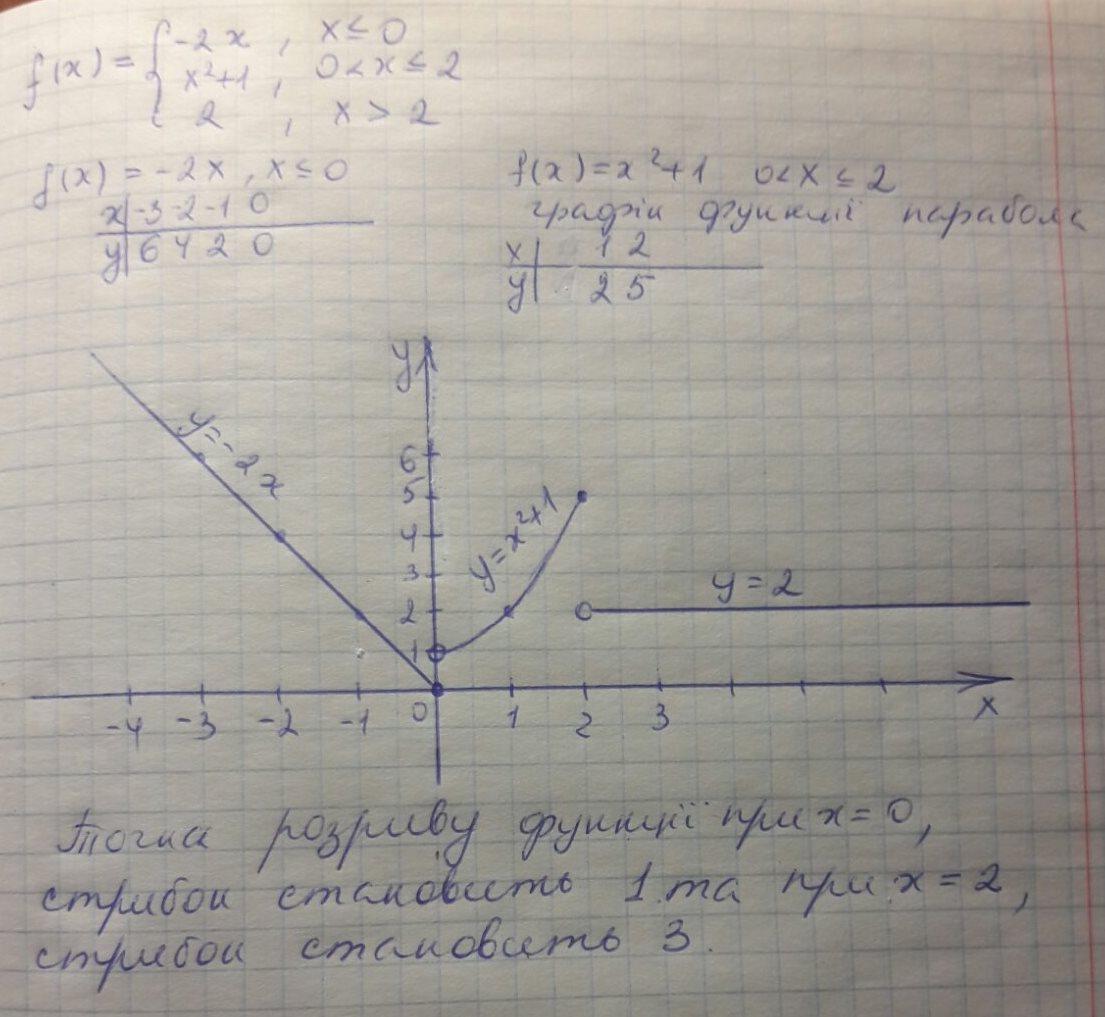
y=-2x - прямая , y=x²+1 - парабола , у=2 - прямая
Точки разрыва проверим на стыках промежутков при х=0 и х=2.
Точка разрыва 1 рода функции при х=0. Скачок равен 1-0=1 .
Точка разрыва 1 рода функции при х=2. Скачок равен 5-2=3.
Приложения:
Автор ответа:
1
Відповідь:
Покрокове пояснення:
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Bsbsbdb
Предмет: Математика,
автор: smeel
Предмет: Алгебра,
автор: kolesnikovanika754
Предмет: Математика,
автор: 1232481
Предмет: Математика,
автор: алинка501