Предмет: Алгебра,
автор: helloiamsuperr
Срочно помогитие 25 баллов матем система уравнений
Приложения:

Ответы
Автор ответа:
3
Ответ: во вложении...
Приложения:
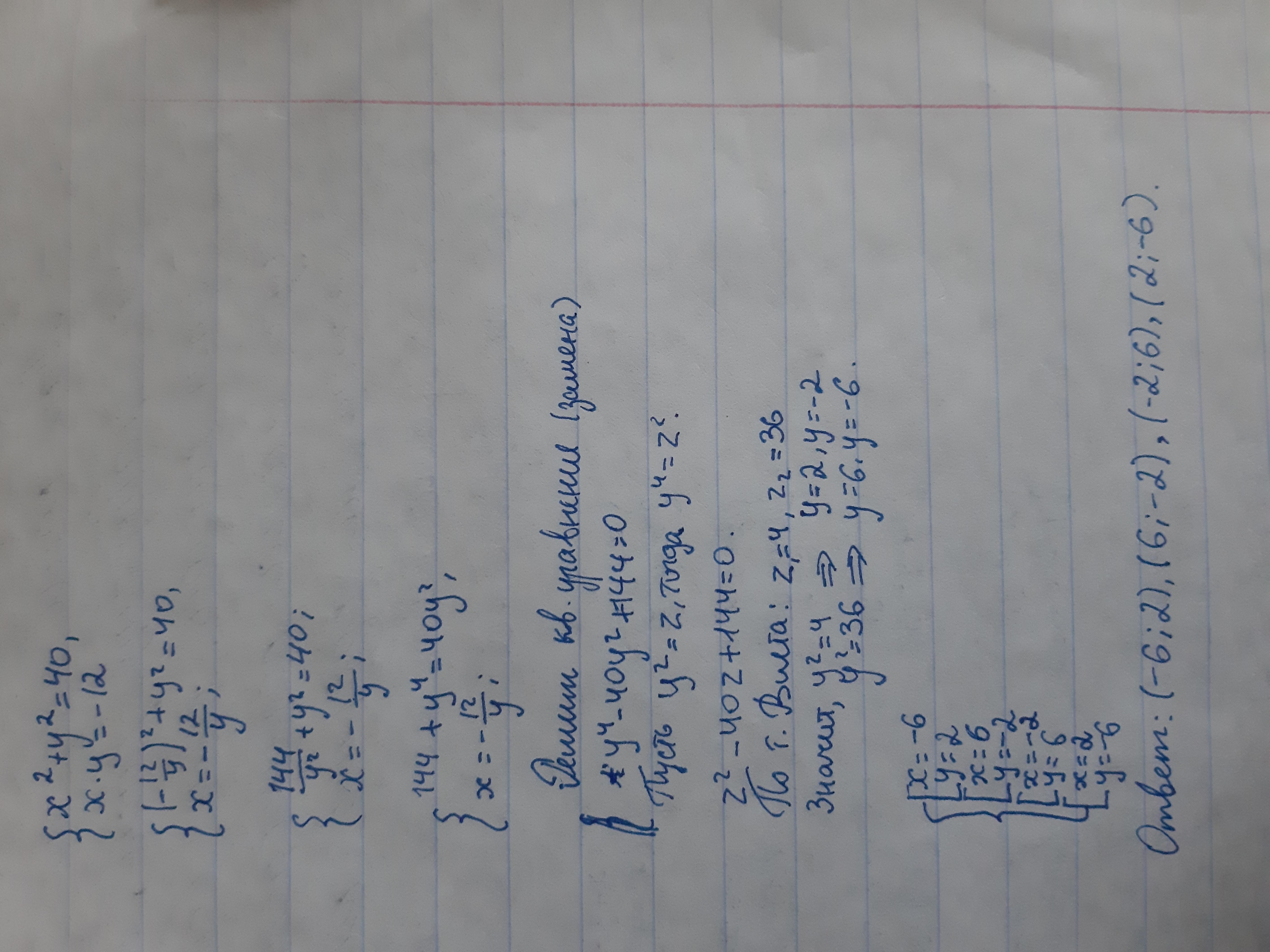
Автор ответа:
1
ОДЗ:
Из второго уравнения выразим
и подставим в первое уравнение:
Так как , получаем биквадратное уравнение:
Замена:
;
Обратная замена:
1)
=>
2) ;
=>
;
А теперь находим
1) При вычисляем
Первое решение готово
2)
Второе решение:
3)
Третье решение:
4)
Четвертое решение:
Ответ:
Похожие вопросы
Предмет: Химия,
автор: darinaminkina2007
Предмет: Українська мова,
автор: kostyksasha2010
Предмет: Українська мова,
автор: dina0098
Предмет: Математика,
автор: Valeriya11111s