Предмет: Математика,
автор: krava9980
5 вопрос. Помогите пожалуйста с ответом, заранее спасибо ))))
Приложения:
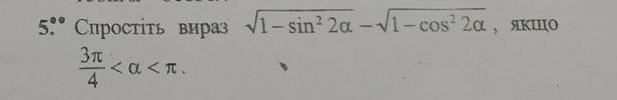
Ответы
Автор ответа:
1
- четвертая четверть
Здесь в четвертой четверти положительный, а
- отрицательный. Следовательно,
Ответ:
iosiffinikov:
Можно еще написать так sqrt(2)*sin(2a+pi/4)
Похожие вопросы
Предмет: Математика,
автор: cifrabonc809
Предмет: Химия,
автор: Kordxeg
Предмет: Алгебра,
автор: i492761
Предмет: Математика,
автор: 2432456
Предмет: Алгебра,
автор: vdash