Предмет: Математика,
автор: natalyabryukhova
F(x) = √(1 - x) + √(x + 3)
Найти максимум функции.
Ответы
Автор ответа:
4
Ответ:
х = -1 - точка максимума, F(-1) = 2√2 - наибольшее значение
Пошаговое объяснение:
ОДЗ: 1 - x ≥ 0
x ≤ 1
x + 3 ≥ 0
x ≥ -3
=> -3 ≤ x ≤ 1
f'(x) = -0,5/√(1-x) + 0,5/√(x+3) = 0
√(x+3) - √(1 - x) = 0, x ≠ 1; x ≠ -3
x + 3 = 1 - x
2x = -2
x = -1 - экстремум
значения производной
___[-3]+++++++[-1]----------[1]__________
т.к. меняются с + на -, то точка максимума
F(-1) = 2√2 - наибольшее значение
F(-3) = 2
F(1) = 2
Автор ответа:
7
Ответ:
векторное решение ( без производной ) :
Пошаговое объяснение:
Приложения:
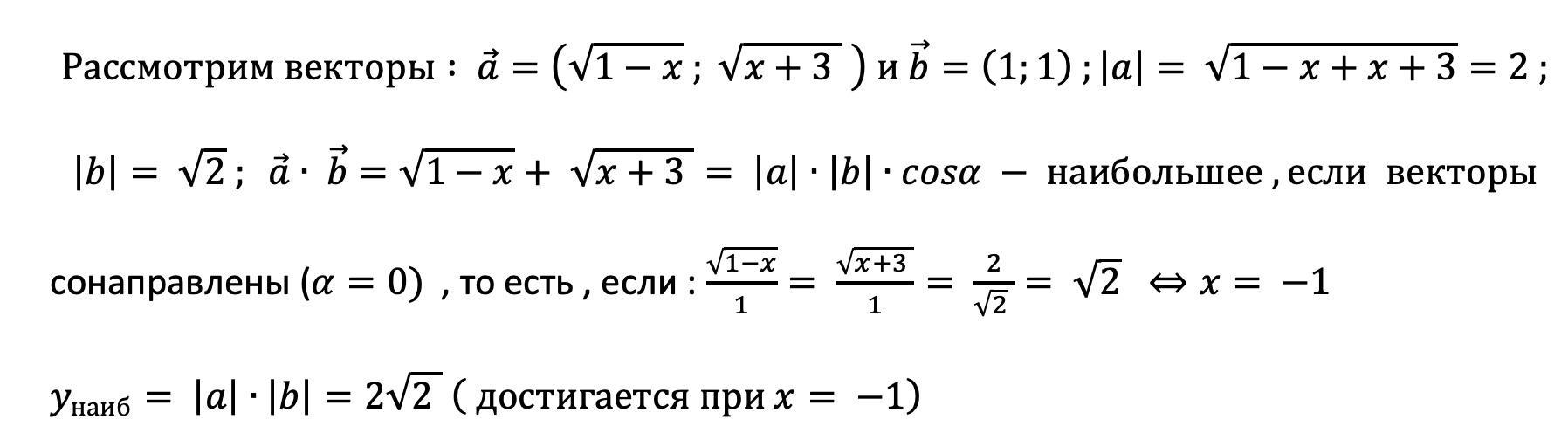
natalyabryukhova:
Спасибо! Очень интересное решение!
Да, красиво.
Но наибольшее не всегда является максимумом. Нет доказательства того, что функция меняет характер с возрастания на убывание при переходе через критич. точки и не ясно, как себя ведет производная.
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Русский язык,
автор: XOFA123
Предмет: Геометрия,
автор: malisenkogeorgij
Предмет: Литература,
автор: doda2284
Предмет: Математика,
автор: АртёмЕлькин