Предмет: Алгебра,
автор: Nurzhan94
Помогите решить ......................................
Приложения:
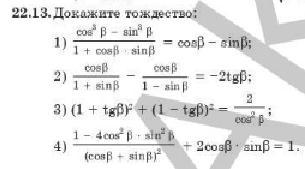
Ответы
Автор ответа:
0
Ответ:
Объяснение:
1)
2)
3)
4)
Похожие вопросы
Предмет: Химия,
автор: TypicalType
Предмет: Алгебра,
автор: yakushenkonatasha098
Предмет: Химия,
автор: Anastatio
Предмет: Математика,
автор: Alina082006
Предмет: Математика,
автор: кристалл22