Предмет: Алгебра,
автор: milanagegel16
Решите тригонометрическое уравнение
Приложения:

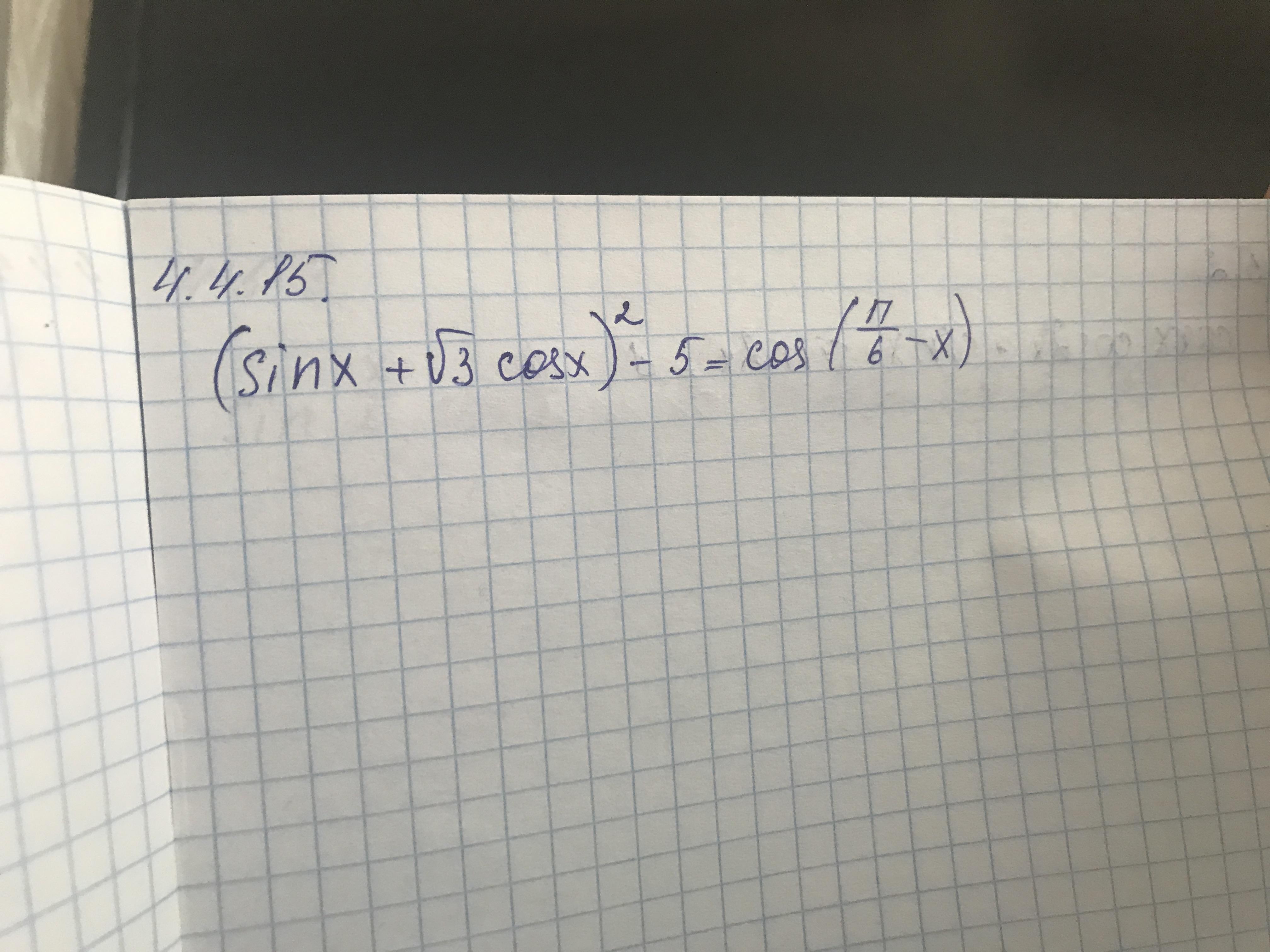
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nazek2405
Предмет: Английский язык,
автор: polinaromaskina13
Предмет: Геометрия,
автор: sskyyleet
Предмет: Физика,
автор: Farhar
Предмет: Химия,
автор: Babobobobooood