Предмет: Математика,
автор: Трахтенберг
Помогите решить:
Найдите значение a, при каждом из которых система уравнений
{ (xy^2 - 2xy - 4y + 8)/√(x+4) = 0
{ y = ax
имеет ровно два различных решения
18 задание из ЕГЭ с параметрами
Приложения:
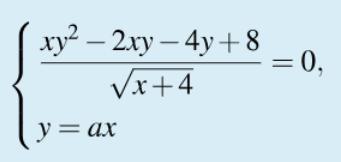
Ответы
Автор ответа:
2
Ответ:
1; 1/2; 1/4
Пошаговое объяснение:
ОДЗ уравнения: х<>4
преобразуем первое уравнение:
подставим y из второго уравнения:
два решения будет в том случае когда пара корней совпадает, или же когда один из корней не удовлетворяет ОДЗ:
совпадать может только корни 1 и 2:
корни 1 и 2 могут не удовлетворять ОДЗ (корень 3 всегда отрицательный).
корень 1:
корень 2:
Похожие вопросы
Предмет: История,
автор: Adilet32
Предмет: Химия,
автор: inga0164
Предмет: Алгебра,
автор: dogn0yobd
Предмет: Математика,
автор: окс113