Предмет: Математика,
автор: LISA78052
Найти интегралы, используя таблицу неопределенных интегралов
Приложения:
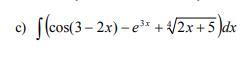
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Математика,
автор: malancukola201
Предмет: Алгебра,
автор: terminatorlolo5
Предмет: Английский язык,
автор: zlatik66
Предмет: Биология,
автор: Аноним
Предмет: Информатика,
автор: 6MissShadow9