Предмет: Алгебра,
автор: cubc201379
Помогите !!!Даю 30 баллов!!! Алгебра!
Найти все значения q ,при которых уравнения x^2-2x+q=0:
1) имеет два различных корня; 2) имеет один корень.
Распишите подробно пожалуйста!!!
Ответы
Автор ответа:
2
Объяснение:
Наше уравнение - квадратное. Найдем его дискриминант:
D = b² - 4ac = (-2)² - 4 · 1 · q = 4 - 4q.
1) квадратное уравнение имеет два различных корня, если его дискриминант - положителен.
Т.е. D > 0, 4 - 4q > 0; 4q < 4 ⇒ q < 1. При таких значениях q уравнение имеет 2 корня.
2) квадратное уравнение имеет один корень, если дискриминант равен 0: D = 0; 4 - 4q = 0; 4q = 4 ⇒ q = 1.
ОТВЕТ: 1) q < 1; 2) q = 1.
Автор ответа:
1
Ответ: решение во вложении.
Объяснение:
Приложения:
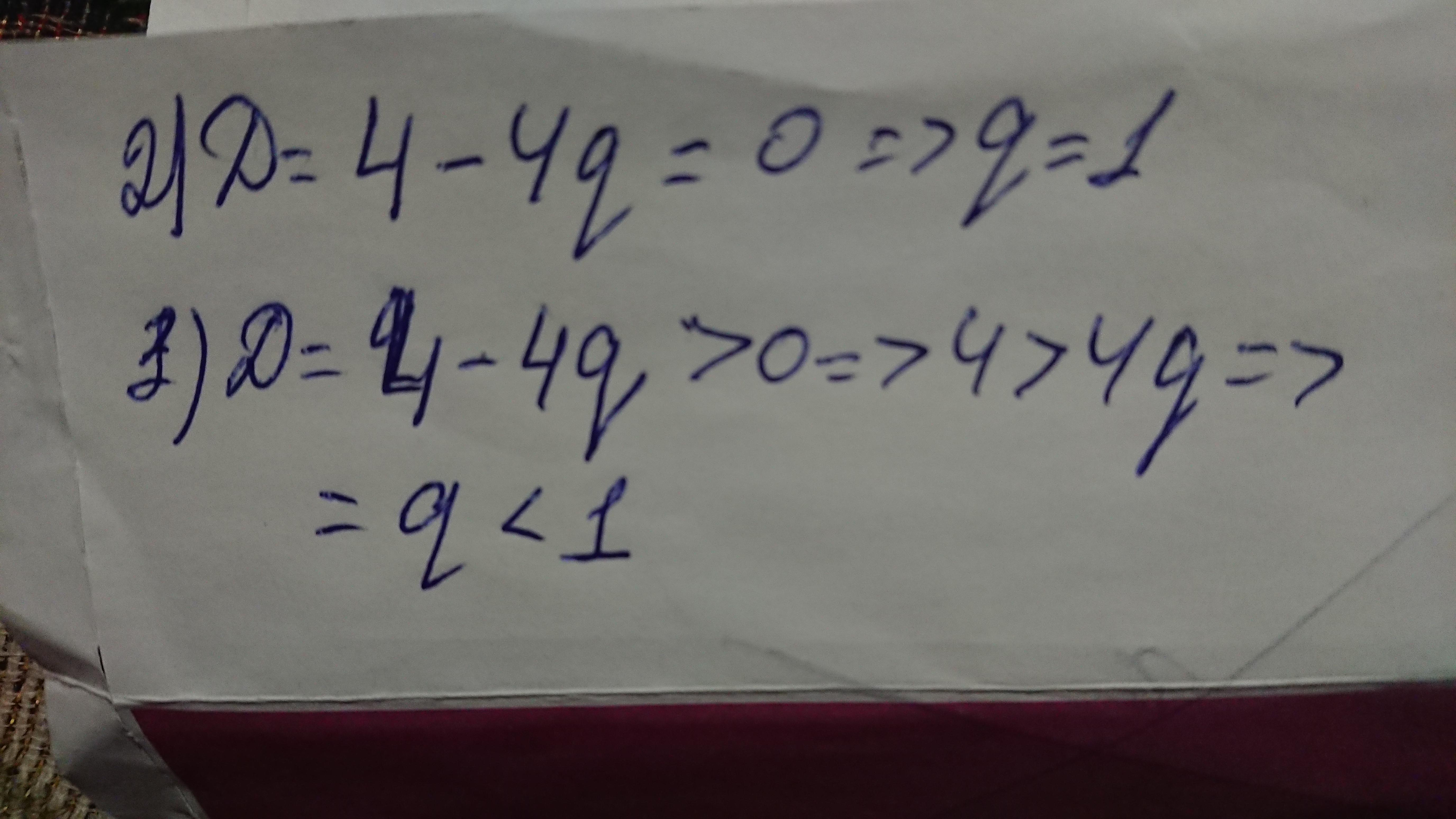
Похожие вопросы
Предмет: Математика,
автор: asttomiriska
Предмет: Английский язык,
автор: ЦейвоЗабув
Предмет: Биология,
автор: sgoow
Предмет: Биология,
автор: Stasia455
Предмет: Алгебра,
автор: mironowajanna2