Предмет: Математика,
автор: nikkimikki200310
Решите неравенство. Даю 50 очков
Приложения:
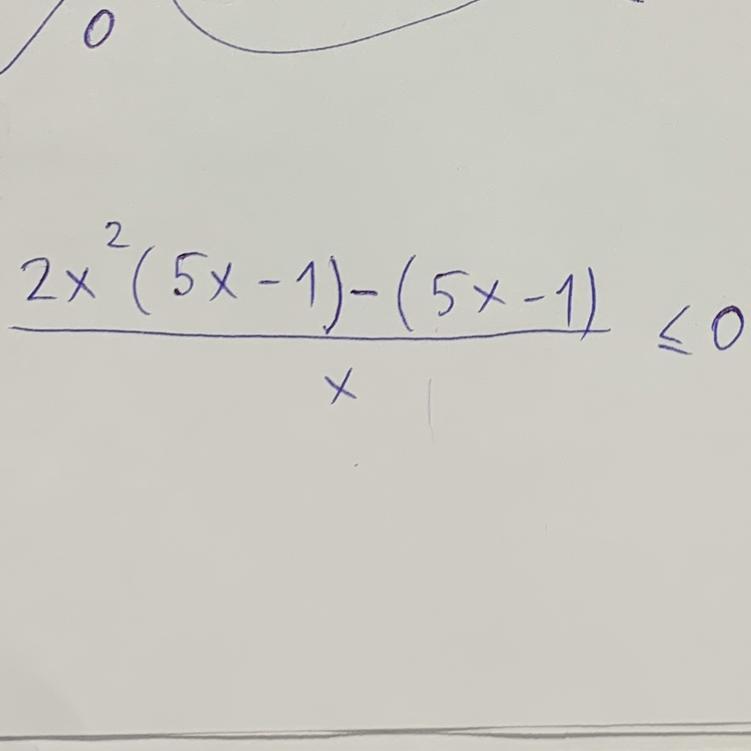
Scythe1993:
как тут решение написать? Задача легкая
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Автор ответа:
1
Ответ:
x∈[)∪[
]
Пошаговое объяснение:
Используя метод змейки, получаем
x∈[)∪[
]
Похожие вопросы
Предмет: Русский язык,
автор: zoyuska9
Предмет: Геометрия,
автор: vv05417
Предмет: Другие предметы,
автор: kornienkodiana120792
Предмет: Литература,
автор: айшилд
Предмет: Информатика,
автор: Hangi