40 баллов
пожалуйста, очень подробно
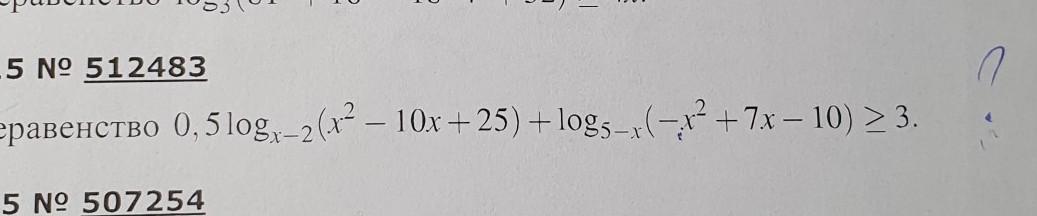
Ответы
Ответ:
x ∈ {3,5}
Пошаговое объяснение:
0,5·logₓ₋₂(x²-10·x+25)+log₅₋ₓ(-x²+7·x-10)≥3
1. Область допустимых значений:
a) x-2>0, x-2≠1, 5-x>0, 5-x≠1 ⇔ 2<x<5, x≠3, x≠4 ⇒ x∈(2; 3)∪(3; 4)∪(4; 5)
b) (x²-10·x+25)>0 ⇔ x≠5, уже учтён
(-x²+7·x-10)>0 ⇔ -(x-2)·(x-5)>0 ⇔ (x-2)·(x-5)<0 ⇔ x∈(2; 5), уже учтён
2. 0,5·2·logₓ₋₂(5-x)+log₅₋ₓ(5-x)·(x-2)≥3
logₓ₋₂(5-x)+log₅₋ₓ(x-2)+log₅₋ₓ(5-x)≥3
logₓ₋₂(5-x)+1/logₓ₋₂(5-x)+1-3≥0
(log²ₓ₋₂(5-x)-2·logₓ₋₂(5-x)+1)/logₓ₋₂(5-x)≥0
(logₓ₋₂(5-x)-1)²/logₓ₋₂(5-x)≥0
Так как (logₓ₋₂(5-x)-1)²≥0, то достаточно рассмотреть случай
logₓ₋₂(5-x)-1=0 ⇔ logₓ₋₂(5-x) = 1 ⇔ 5 - x = x - 2 ⇒ x =3,5 ∈ (2; 3)∪(3; 4)∪(4; 5)
Тогда, если при x ≠3,5 получим следующее равносильное неравенство
logₓ₋₂(5-x)>0 ⇔ logₓ₋₂(5-x)>logₓ₋₂1
a) 0<2-x<1 ⇔ 1<x<2 ⇔ x ∈(1; 2):
5-x<1 , x ∈(1; 2) ⇔ 4<x, x ∈(1; 2) ⇒ x∈∅
b) 2-x>1 ⇔ x < 1 ⇔ x ∈(-∞; 1):
5-x>1 , x ∈(-∞; 1) ⇔ x<4, x ∈(-∞; 1) ⇒ x ∈(-∞; 1). Но в силу ОДЗ, также x∈∅.