Предмет: Алгебра,
автор: Аноним
Решить качественно и более-менее понятно.
Приложения:
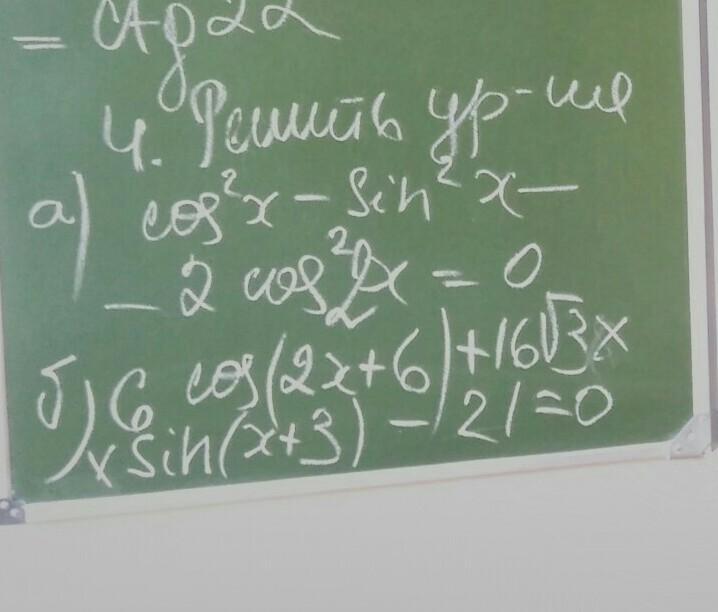
Ответы
Автор ответа:
2
dasew12:
Здравствуйте. помогите пожалуйста https://znanija.com/task/34073332?answeringSource=feedPersonal%2FhomePage%2F2
Помогите пожалуйста https://znanija.com/task/34076004
Автор ответа:
2
Ответ: во вложении Объяснение:
Приложения:

Помогите пожалуйста
https://znanija.com/task/34076004
https://znanija.com/task/34076004
Похожие вопросы
Предмет: Математика,
автор: timadragsony2009
Предмет: Українська мова,
автор: mekantop123
Предмет: История,
автор: dd919929
Предмет: Математика,
автор: таня1556
Предмет: Математика,
автор: snezhanaastani