Предмет: Алгебра,
автор: totoshka1980
Помогите пожалуйста упростить выражение
Приложения:
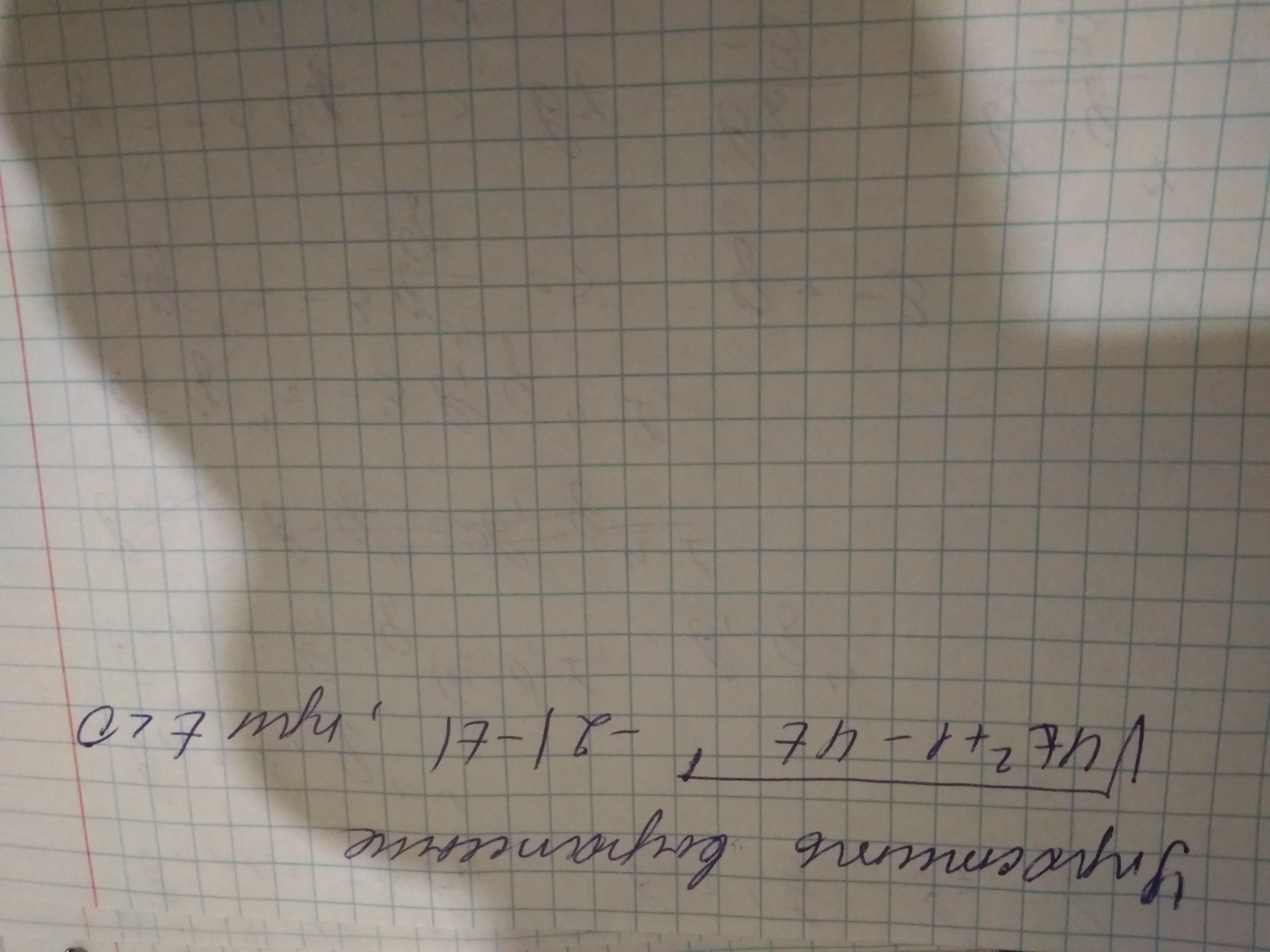
Ответы
Автор ответа:
2
Ответ:
1
Объяснение:
t<0, значит t - число отрицательное.
Обозначим его -t.
Тогда
4(-t)²=4t, т.к. любое число, возведенное в четную степень есть число неотрицательное.
-4(-t)=4t, т.к. отрицательное число, умноженное на отрицательное, есть число положительное.
-(-t)=t, т.к. число в скобках нужно взять с противоположным знаком.
Получаем
Под знаком корня выделяем полный квадрат.
|t|=t, т.к. неотрицательное число по модулю есть само это число.
Значит
В нашей записи t - число неотрицательное, поэтому выражение под знаком модуля будет больше нуля. Знак модуля опускаем.
.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Українська мова,
автор: 628293050500393
Предмет: География,
автор: ugnivenkodanilo
Предмет: Математика,
автор: 200921
Предмет: Математика,
автор: maksik29