Предмет: Алгебра,
автор: AiSamBaku555
Помогите решить уравнение.
Приложения:
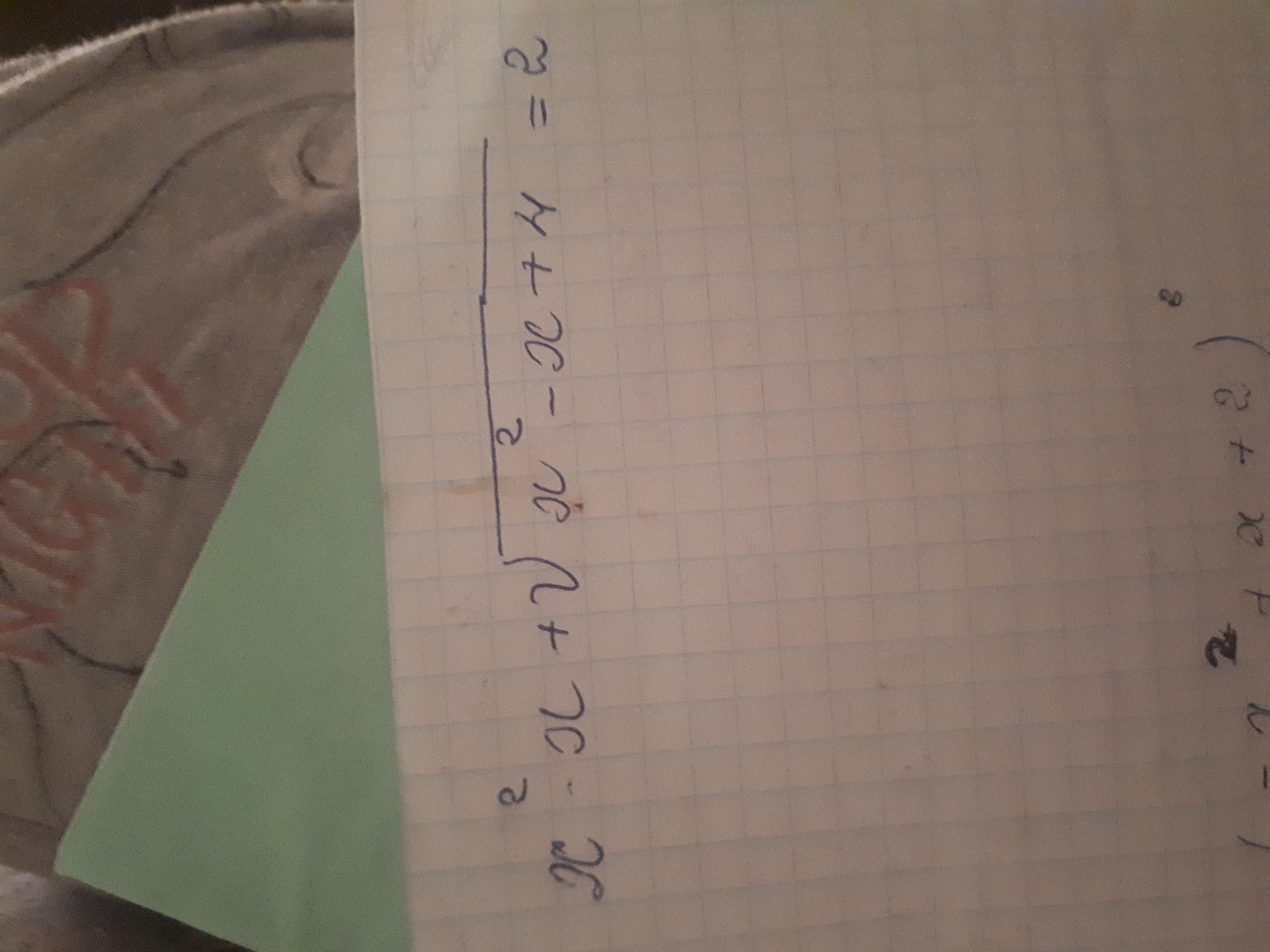
Ответы
Автор ответа:
1
Universalka:
Проверкой убеждаемся, что подходят оба корня.
помоги ещё рах
*раз*
Похожие вопросы
Предмет: Английский язык,
автор: asavugman420
Предмет: Математика,
автор: Artemyj
Предмет: Українська мова,
автор: yosypiv18
Предмет: География,
автор: Аноним
Предмет: География,
автор: anellya1