Question

МОГУ ДАТЬ БОЛЬШЕ БАЛЛОВ​

Answer 1

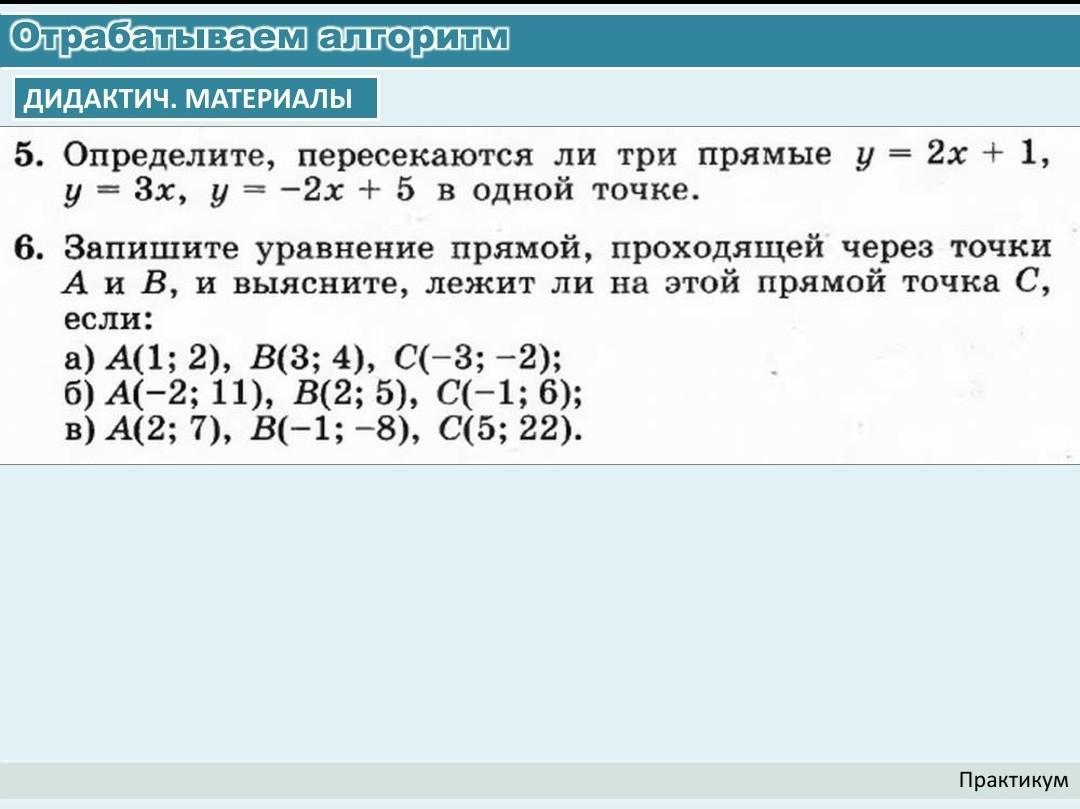
5.

у = 2х + 1,

у = 3х,

у = -2х + 5,

точка пересечения 1 и 2 прямых:

2х + 1 = 3х,

2х - 3х = -1,

х = 1,

у = 2х+1 = 2*1+1 = 3,

или:

у = 3*1 = 3       ⇒       (1; 3),

точка пересечения 1 и 3 прямых:

2х + 1 = -2х + 5,

2х + 2х = 5 - 1,

4х = 4,

х = 1,

у = 2х+1 = 2*1+1 = 3,

или:

у = -2*1+5 = -2+5 = 3       ⇒       (1; 3),

значит все три прямые пересекаются в точке  (1; 3),

6.

уравнение прямой, которая проходит через две заданные точки:

х - х₁        у - у₁

-------  =  ---------   ,

х₂ - х₁       у₂ - у₁

а)

(х - 1) / (3 - 1) = (у - 2) / (4 - 2),

(х - 1) / 2 = (у - 2) / 2,

х - 1 = у - 2,

х - у + 1 = 0,

подставим координаты точки С:

-3 + 2 + 1 = 0,

0 = 0 - точка С (-3; -2) лежит на прямой,

б)

(х + 2) / (2 + 2) = (у - 11) / (4 - 11),

(х + 2) / 4 = (у - 11) / (-7),

-7(х + 2) = 4(у - 11),

-7х - 14 = 4у - 44,

-7х - 4у - 14 + 44 = 0,

7х + 4у - 30 = 0,

подставим координаты точки С:

-7*(-1) + 4*6 - 30 = 0,

7 + 24 - 30 = 0,

1 ≠ 0 - точка С (-1; 6) не лежит на прямой,

в)

(х - 2) / (-1 - 2) = (у - 7) / (-8 - 7),

(х - 2) / (-3) = (у - 7) / (-15),

5(х - 2) = у - 7,

5х - 10 - у + 7 = 0,

5х - у - 3 = 0,

координаты точки С:

5*5 - 22 - 3 = 0,

25 - 22 - 3 = 0,

0 = 0 - точка С (5; 22) лежит на прямой