Геометрия 11 класс. Срочно!!!
Всё дано на рисунке
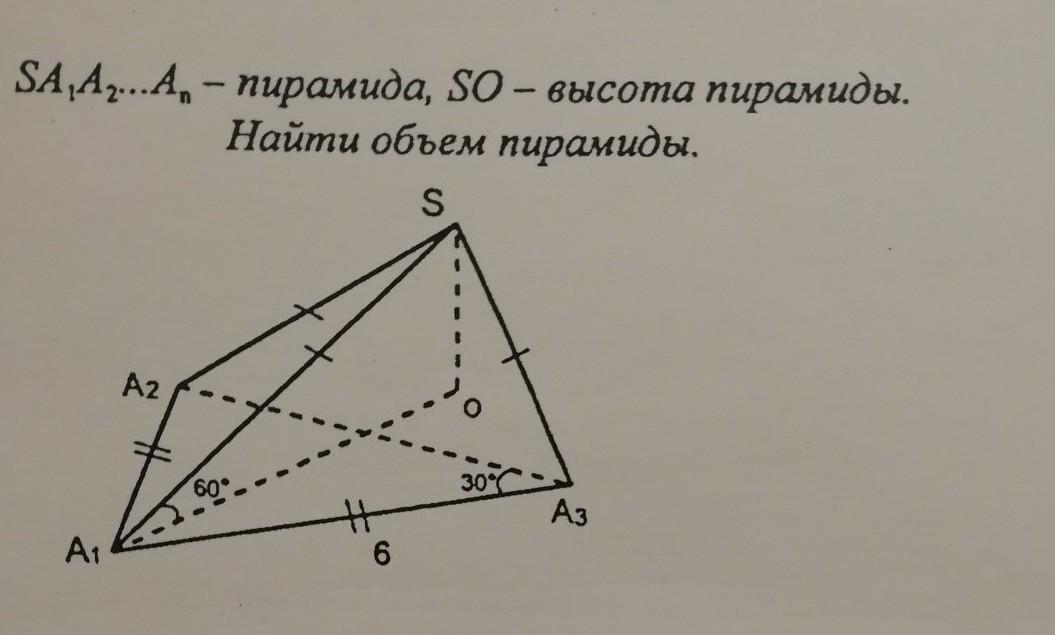
Ответы
Ответ: 54
Объяснение:
Поскольку SO высота , то прямоугольные треугольники
ΔA2OS =ΔA3OS=ΔA1OS по равным гипотенузам A2S=A3S=A1S и общей высоте SO .
Откуда A2O=A3O=A1O
Теперь смотрите на рисунок , что я вложил. ( он посвящен четырехугольнику A1A2A3O)
ΔA1A3O=ΔA1A2O - по трем сторонам
Тогда
∠SA1A3=∠SA1A2 , то есть A1S - биссектриса угла A1 равнобедренного треугольника A3A1A2 , но тогда она же и его высота .
Таким образом ∠A3SA1=90
Тогда : ∠SA1A3=90-60 =30
ΔOA1A3- равнобедренный , тогда ∠OA3A1=∠OA1A3=60 , то и его третий угол : 180-60-60=60 , таким образом ΔOA1A3 - равносторонний . То есть A10=6
Возвращаемся к начальному чертежу.
Из прямоугольного Δ A1SO определяем высоту h=SO
h= 6* tg(60) = 6*√3
∠A1=2*60=120
Определим площадь основания S= SΔA1A2A3= 1/2 *6^2 *sin(120)= =18*√3/2 =9*√3
Объем пирамиды :
V=1/3 *s*h =1/3 *9√3 *6*√3 = 54
Ответ: 54
