Предмет: Математика,
автор: htytroro
Найти радиус сходимости ряда
Приложения:
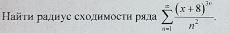
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: galitskiji
Предмет: Литература,
автор: solomiavaschyk07
Предмет: Литература,
автор: rafaelevnaregina581
Предмет: Биология,
автор: devchonka238
Предмет: Алгебра,
автор: misissbond