Question

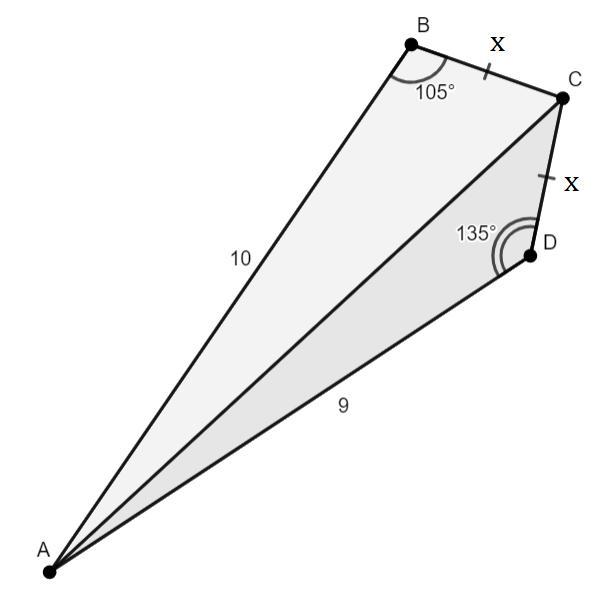
Участок земли имеет форму выпуклого четырехугольника ABCD, в котором AB=10м, AD=9м. BC=CD, Угол B=105°, Угол D=135°. Найдите с точностью до 0.1м^2 площадь этого участка.

Answer 1

Пусть BC = CD = x м

По теореме косинусов в ΔABC:

$AC^2=AB^2+BC^2-2AB\cdot BC\cdot \cos{(ABC)}\\\\AC^2=10^2+x^2-2\cdot 10\cdot x\cdot \cos{105^\circ }$

cos 105° = cos(45°+60°) = cos(45°)·cos(60°)-sin(45°)·sin(60°) = $\dfrac{\sqrt2}2 \cdot \dfrac12 -\dfrac{\sqrt2}2 \cdot \dfrac{\sqrt3}2 =\dfrac{\sqrt2-\sqrt6}4$

По теореме косинусов в ΔACD:

$AC^2=AD^2+CD^2-2AD\cdot CD\cdot \cos{(ADC)}\\\\AC^2=9^2+x^2-2\cdot 9\cdot x\cdot \cos{135^\circ }$

cos 135° = cos(90°+45°) = -sin45° = $\dfrac{-\sqrt2}2$

Приравняем значения AC² и найдём х.

$100+x^2-20x\cdot \dfrac{\sqrt2 -\sqrt6}4 =81+x^2-18x\cdot \left( \dfrac{-\sqrt2}2 \right) \\\\19=5\! \left(\sqrt2 -\sqrt6\right) x+9\sqrt2 \,x\\\\\left( 5\sqrt2 -5\sqrt6 +9\sqrt2 \right) x=19\\\\x=\dfrac{19}{14\sqrt2 -5\sqrt6}$

• Площадь треугольника равна полупроизведению длин двух сторон на синус угла между ними.

$S_{ABC} =\dfrac{AB\cdot BC}2 \cdot \sin{(ABC)} =\dfrac{10x}2 \cdot \sin{105^\circ}$

sin 105° = sin(45°+60°) = sin(45°)·cos(60°)+cos(45°)·sin(60°) = $\dfrac{\sqrt2}{2} \cdot \dfrac12 +\dfrac{\sqrt2}2 \cdot \dfrac{\sqrt3}2 =\dfrac{\sqrt2 +\sqrt6}4$

$S_{ACD} =\dfrac{AD\cdot CD}2 \cdot \sin{(ADC)} =\dfrac{9x}2 \cdot \sin{135^\circ }$

sin 135° = sin(90°+45°) = cos45° = $\dfrac{\sqrt2}2$

$S_{ABCD} =S_{ABC} +S_{ACD} =\dfrac{10x}2 \cdot \dfrac{\sqrt2 +\sqrt6}4 +\dfrac{9x}2 \cdot \dfrac{\sqrt2}2$

$S_{ABCD} =\dfrac{5\sqrt2 +5\sqrt6 +9\sqrt2 }4 \cdot x=\dfrac{14\sqrt2 +5\sqrt6}4\cdot \dfrac{19}{14\sqrt2 -5\sqrt6} =\\\\=\dfrac{19}4 \cdot \dfrac{\left( 14\sqrt2 +5\sqrt6 \right) ^2}{\left( 14\sqrt2 -5\sqrt6 \right) \left( 14\sqrt2 +5\sqrt6 \right) } =\dfrac{19}4 \cdot \dfrac{\left( 14\sqrt2 \right) ^2+2\cdot 14\sqrt2\cdot 5\sqrt6+\left( 5\sqrt6 \right) ^2}{\left( 14\sqrt2 \right) ^2-\left( 5\sqrt6 \right) ^2} =\\\\=\dfrac{19}4 \cdot \dfrac{392+280\sqrt3 +150}{392-150} =\dfrac{19(271+140\sqrt3)}{484}$

$S_{ABCD} =\dfrac{5149+2660\sqrt3 }{484} \approx 20,\! 2$

Ответ: 20,2 м².