Предмет: Математика,
автор: gfhddtukjvcd
найти производную, только если можете, напишите подробно. Буду благодарен! :)
Приложения:
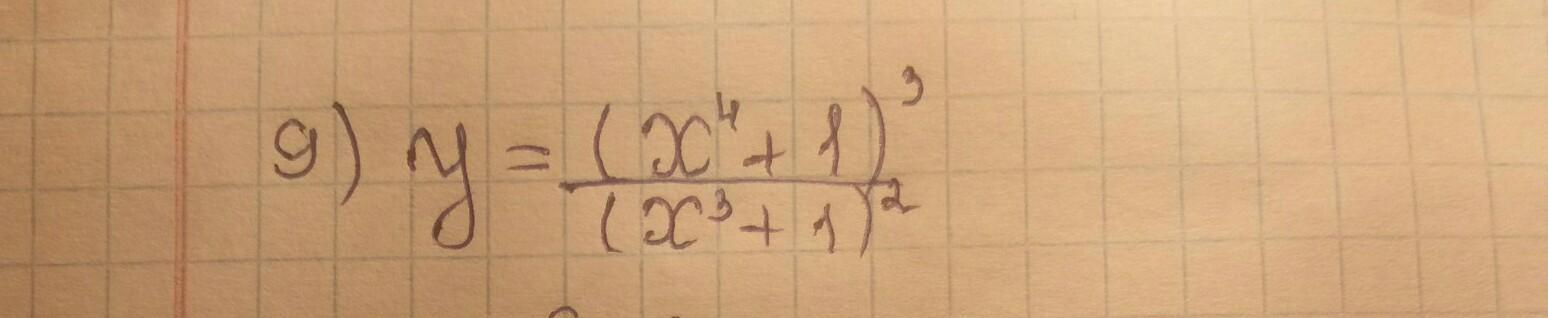
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
ytgfvciiwowieu:
Помоги мне прошу те
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
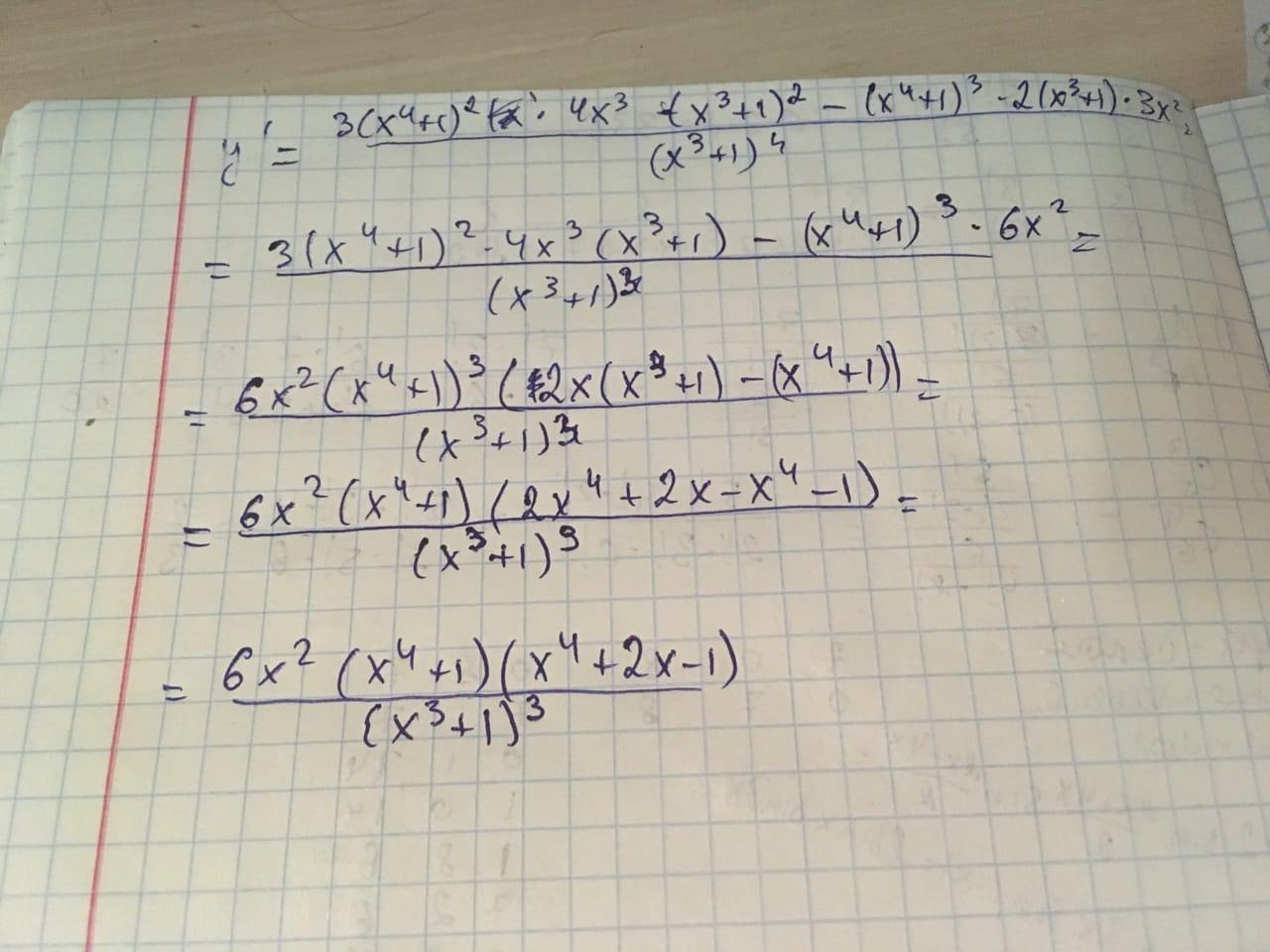
спасибо большое!! а почему вышли разные ответы с преведущим ответом? У кого правильно?
они одинаковые, просто можно еще немного попреобразовывать
понял, спасибо)
Похожие вопросы
Предмет: Биология,
автор: evaboro18
Предмет: Математика,
автор: aklololoska
Предмет: Қазақ тiлi,
автор: koksetaumecta07
Предмет: Алгебра,
автор: ananasanastasia