Предмет: Алгебра,
автор: marileschins83
Целые рациональные уравнения,пожалуйста
Приложения:
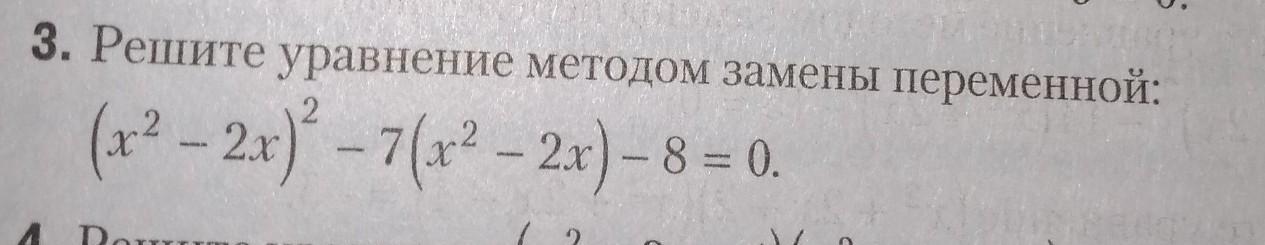
Ответы
Автор ответа:
2
Ответ:
{-3;4}
Объяснение:
Заменим одинаковые значение на t:
, t ≥0 (*)
Уравнение приобретает вид:
Решаем через дискриминант
Находим корни
Второй корень не удовлетворяет условие (*)
Обратная замена
Решаем оба уравнения:
В первом уравнении корней нет из-за отрицательного дискриминанта
Находим корни
marileschins83:
спасибо,но неправильно)
Похожие вопросы
Предмет: Другие предметы,
автор: shyraizhumazhan
Предмет: Українська мова,
автор: dianalukianets
Предмет: Литература,
автор: les0ja30kunyzkaja200
Предмет: Математика,
автор: werg777