Предмет: Математика,
автор: LamaDayKappa
Найти предел функции
Приложения:
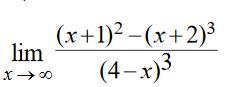
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: myaroslavcki
Предмет: Алгебра,
автор: vasylynakupin
Предмет: Алгебра,
автор: jasmina1608200936
Предмет: Литература,
автор: rose841
Предмет: Математика,
автор: feduevang