Предмет: Математика,
автор: ЭмилиСтоун11
Пожалуйста помогите решить
Приложения:
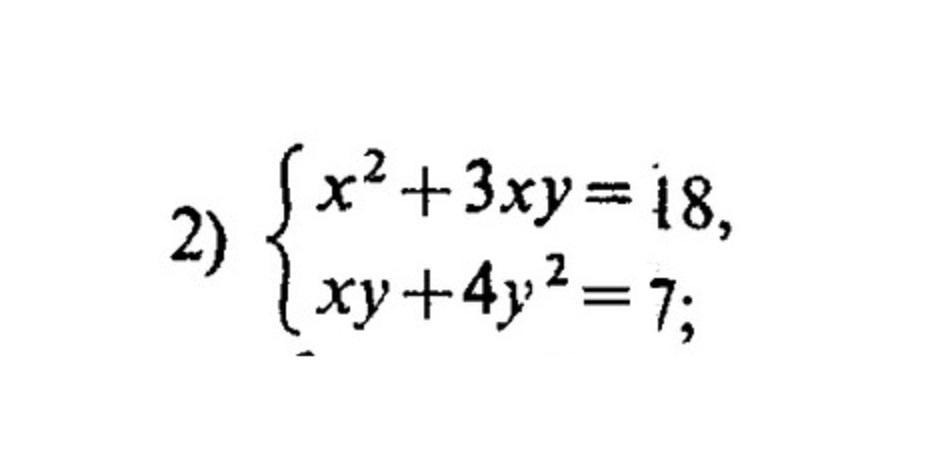
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Математика,
автор: galileogaliley97
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: k0682743734
Предмет: Литература,
автор: ромашка166
Предмет: Алгебра,
автор: УчительМужик