пожалуйста помогите
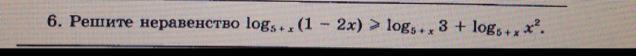
Ответы
Ответ:
x∈(-5; -4)∪(-1; 1/3)
Пошаговое объяснение:
log₅₊ₓ(1-2·x)>log₅₊ₓ3+log₅₊ₓx²
Область допустимых значений неравенства:
5+x>0, 5+x≠1, 1-2·x>0, x²>0 равносильно
x>-5, x≠-4, x<1/2, x≠0 равносильно
x∈(-5; -4)∪(-4; 0)∪(0; 1/2).
Тогда
log₅₊ₓ(1-2·x)>log₅₊ₓ3·x²
1) Пусть сначала 0<5+x<1 или -5 < x < -4 или x∈(-5; -4):
1-2·x<3·x²
3·x²+2x-1>0
Рассмотрим квадратное уравнение 3·x²+2x-1=0.
D=2²-4·3·(-1)=4+12=16=4²
x₁ = (-2-4)/(2·3) = -1
x₂ = (-2+4)/(2·3) = 1/3
Тогда неравенство 3·x²+2x-1>0 равносильно к неравенству
3·(x-1/3)·(x+1)>0. Применим метод интервалов, определим знак
3·(x-1/3)·(x+1) + - +
-∞ ---------------------(-1)--------------(1/3)---------------------------> +∞
Отсюда, x∈(-∞; -1) ∪ (1/3; +∞) и учитывая x∈(-5; -4) получим: x∈(-5; -4).
2) Пусть теперь 5+x>1 или x > -4 или x∈(-4; +∞):
1-2·x>3·x²
3·x²+2x-1<0
Из 1) получим
3·(x-1/3)·(x+1) + - +
-∞ ---------------------(-1)--------------(1/3)---------------------------> +∞
Отсюда, x∈(-1; 1/3) и учитывая x∈(-4; +∞) получим: x∈(-1; 1/3).
Ответ: x∈(-5; -4)∪(-1; 1/3).