Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста, напишите как решать... лучше с графиком
Найти площадь фигуры, ограниченной параболой y= -x^2+4x-3 и прямой, проходящей через точки (1,0) и (0,-3)
Ответы
Автор ответа:
5
Ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
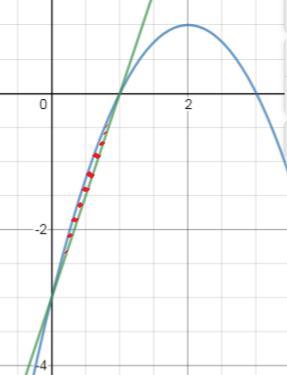
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
Искомая площадь - S = 1/6 (кв. ед)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: arminarlert22869009
Предмет: Алгебра,
автор: fox6280
Предмет: Українська мова,
автор: Аноним
Предмет: Литература,
автор: edikru21
Предмет: История,
автор: so8n8ya