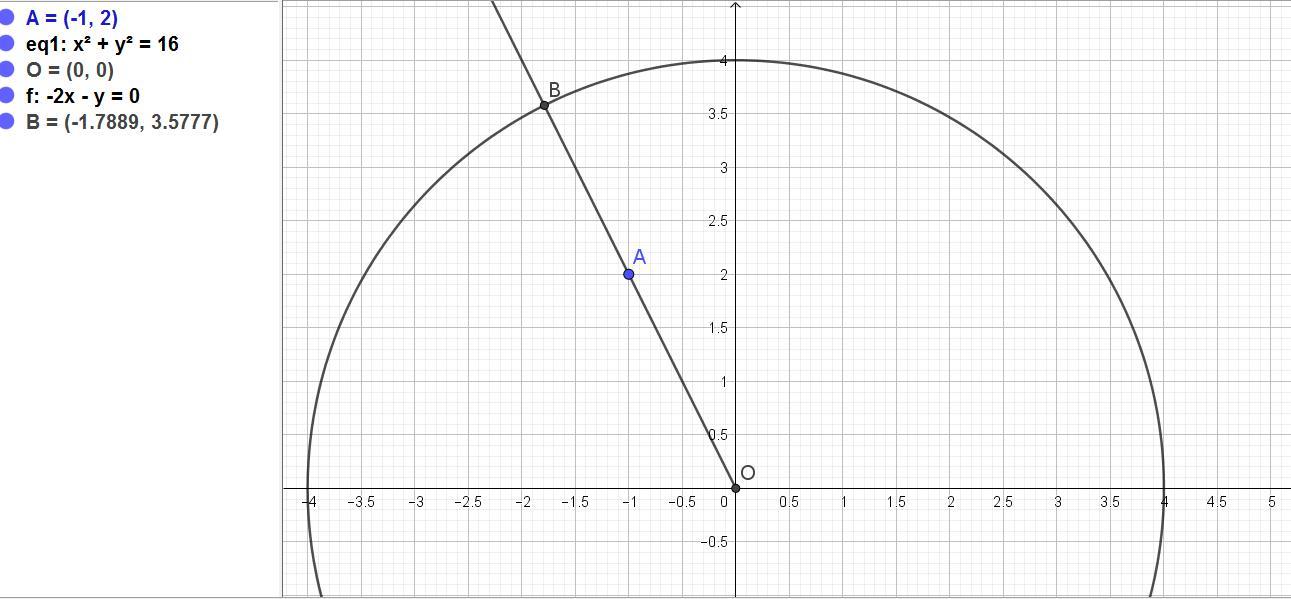
Найти расстояние от точки (-1;2) до кривой х^2+у^2=16.
Ответы
Даны точка А(-1; 2) и кривая x² + y² = 16.
Квадрат расстояния между двумя точками определяется соотношением d²=(x1−x2)²+(y1−y2)². Так как надо найти расстояние от точки до кривой, то координаты второй точки (лежащей на кривой) должны удовлетворять ее уравнению, поэтому d²=(x1−x2)²+(y1−f(x2))²=
= (x + 1)² + (√(16 - x²) - 2)² = x² + 2x + 2 + 16 - x² - 4√(16 - x²) + 4 =
= 2x −4√(16 - x²) + 20.
Расстояние от точки до кривой - это минимальное расстояние между двумя точками, одна их которых лежит на кривой. Тогда для нахождения расстояния нам надо найти минимум функции определяющей расстояние, то есть, найти ее производную и приравнять нулю.
(d²)′ = 2(√(16 - x²) + 2x) / √(16 - x²).
Приравняем нулю числитель (можно выражение в скобках).
√(16 - x²) + 2x = 0 или √(16 - x²) = -2x.
Отсюда вывод: знак переменной х отрицателен.
Возведём обе части в квадрат.
16 - x² = 4x²,
5x² = 16, отсюда х = +- 4/√5, но у нас х = -4√5.
Находим у = +-√(16 - x²), но так как точка А имеет ординату с плюсом, то и ближайшая точка на кривой тоже с плюсом.
у = √(16 - (-4/√5)²) = √(16 - (16/5)) = √(64/8) = 8/√5.
Расстояние находим по вышеприведенной формуле.
d² = (-4/√5) - (-1))² + (8/√5 - 2)² = 21 - 8√5.
d = √(21 - 8√5) = √(16 - 8√5 + 5) = √(4 - √5)² = 4 - √5 ≈ 2,236.
Эту задачу можно было решить проще.
Заданная кривая x² + y² = 16 это окружность с центром в начале координат и радиусом 4.
Ближайшая точка лежит на одном радиусе ОА.
ОА = √(-1 - 0)² +(2 - 0)² = √5.
Ответ: d = 4 - √5.