Question

ПОЖАЛУСТО ДАЮ 35 БАЛОВ
ЯКЩО З ПОЯСНЕННЯМИ



основа і бічна сторона рівнобедреного трикутника відносяться як 6: 5.знайдіть
радиус описаного кола, якщо периметр трикутника дорівнює
64 дм.​

Answer 1

Розв'язання.

Основа і бічна сторона рівнобедреного трикутника відносяться як 6:5 => Нехай основа дорівнює 6х, тоді бічна сторона дорівнює 5х.

Периметр даного трикутника дорівнює 64 дм, отже, отримаємо рівняння:

5х+5х+6х=64;

16х=64;

х= 4.

Звідси основа дорівнює 6×4=24 дм, а бічна сторона 5×4=20 дм.

Радіус описаного навколо трикутника кола дорівнює

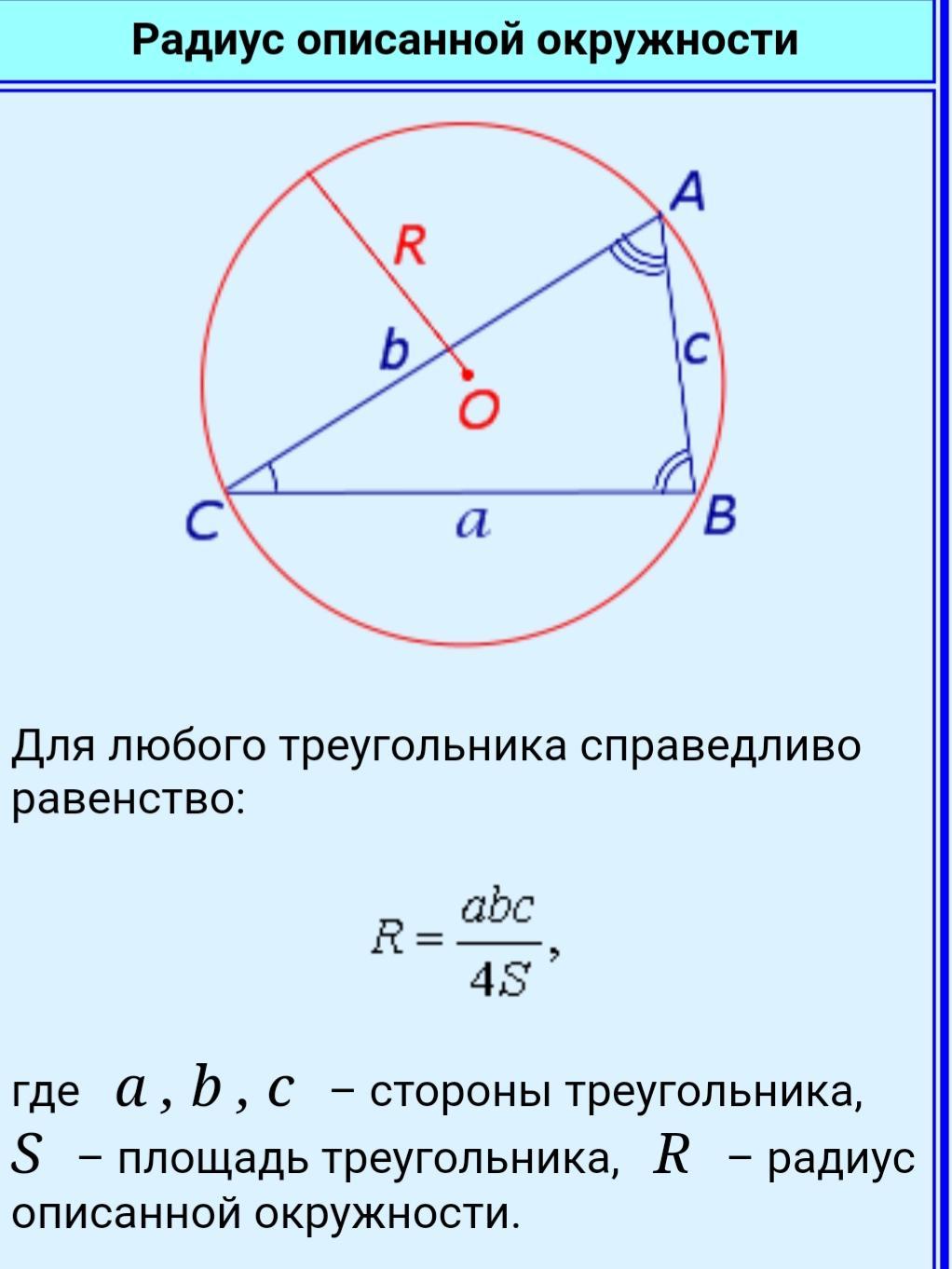
R= abc/4S, де a, b і с - сторони трикутника, S - його площа, а R - радіус описаного навколо цього трикутника кола.

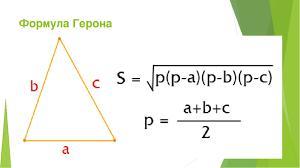
Для початку потрібно знайти площу трикутника (формула Герона, дивитись на скріншоті, я одразу підставляю значення):

p= ½P= 64÷2=32 дм.

S²= 32(32-20)(32-20)(32-24);

S²= 32×12×12×8;

S²= 12²×256;

S²=12²×16²;

S=12×16=192 (дм²).

Тепер знайдемо радіус.

R= 24×20×20 / 4×192;

R= 6×400 / 192;

R= 400/32;

R= 12,5 (дм)

Відповідь: 12,5 дм.

Во вложении:

1. Формула площади треугольника

2. Формула нахождения радиуса описанной около треугольника окружности.