Предмет: Алгебра,
автор: zombiede98
Исследовав систему на совместность, найти ее общее решение методом Гаусса.Помогите решить с подробным объяснением.
Приложения:
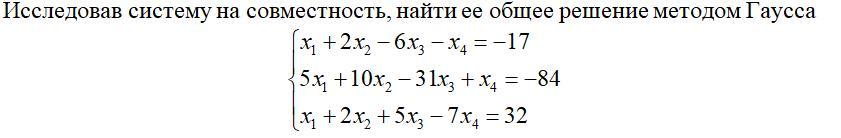
Ответы
Автор ответа:
1
Ответ:
Ранг матрицы системы равен рангу расширенной матрицы системы и равен r=3. Значит, по теореме Кронекера-Капелли система совместна. Количество неизвестных равно n=4. Так как r<n , то система имеет бесчисленное множество решений. Выбираем базисные неизвестные - это х₂ , х₃ , х₄ (определитель матрицы, составленной из коэффициентов перед этими неизвестными, не равен 0) и свободное неизвестное x₁ , которое может принимать произвольные числовые значения. Выражаем базисные неизвестные через свободное.
ZombieDe:
как в данной матрице увидеть ранги?
ранг = количеству строк в матрице ступенчатого вида
спасибо!
Похожие вопросы
Предмет: Английский язык,
автор: nseraa77
Предмет: Английский язык,
автор: Adik0070731
Предмет: Қазақ тiлi,
автор: onalbekovaakerke264
Предмет: Математика,
автор: heyIniiko
Предмет: Алгебра,
автор: агафья4