РЕШИТЕ ЗАДАНИЕ!!МНОГО БАЛЛОВ!!ДА ЕЩЕ И ПОДСКАЗКА БОЛЬШАЯ ЕСТЬ ДЛЯ РЕШЕНИЯ!!!!
Само задание:
Клетчатая доска 9×9 покрашена в шахматную раскраску (то есть доска покрашена в чёрный и белый цвета; любые две клетки, соседние по
стороне, имеют разный цвет). Требуется поставить 8 белых ладей так,
чтобы все они стояли на клетках одного цвета и никакие две из них
не били друг друга (одна ладья бьёт другую, если она стоит с ней в
одной вертикали или горизонтали). Сколькими способами это можно
сделать? Расстановки, отличающиеся друг от друга поворотами, симметриями и пр. считаются различными
Подсказка для него:
Пусть угловые клетки - белые.
1) Ладьи на белых клетках.
Удаляем одну из 9 горизонталей, где ладьи не будет. Поскольку горизонтали различаются, выделим два случая, в зависимости от первой клетки горизонтали: а) белая, б) чёрная.
Далее проходим по белым горизонталям, выбирая место для ладей: на первой из белых горизонталей - 5 мест, затем - 4 места и т. д. Аналогично поступаем с чёрными горизонталями.
2) Ладьи на чёрных клетках.
Аналогично. Частично можно свести к предыдущему пункту.
Пробовал решать :
Для первой ладьи - 8 вариантов, для второй - 7 вариантов и т. д. В итоге 8!
Еще раз пересчитал. Число расстановок 8-ми ладей на одноцветных полях равно 9*5!*4!+5*5!*4!=14*5!*4!=8!(первое слагаемое отвечает за цвет, совпадающий с цветом угловых клеток, второе - за другой цвет)
Потом у меня получилось посчитать это по-другому: 9 способов убрать 1 лишнюю горизонталь * 9 способов убрать лишнюю вертикаль (т.к. ладей 8, то на поле 9*9 всегда такие лишние найдутся) * кол-во способов расставить их по чёрным и по белым клеткам (т.е. 4! + 4!), получим 9*9 * (4! + 4!) = 3888 способов.
Позже исправил : 9*9 * (4!*4! + 4!*4!) = 93 312(по белым на поле 8*8 кол-во способов 4! * 4! + аналогично для чёрных)
Я уже запутался со всем этими расчетами , помогите пожалуйста
Ответы
Ответ:
40320
Пошаговое объяснение:
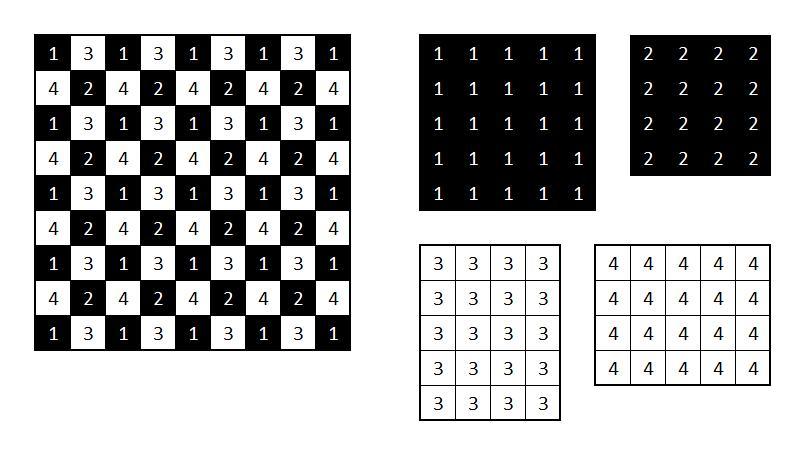
У меня угловые клетки черные, это, конечно, ни на что не влияет. Рассматриваем два варианта - на черных клетках стоят ладьи или на белых. Потом результаты сложим и получим ответ.
1. Белые клетки
Если внимательно посмотреть на доску, белые клетки делятся на две независимые (с точки зрения хода ладьи) группы, помеченные у меня цифрами 3 и 4. Я перерисую их отдельно, получатся прямоугольники 4x5 и 5x4. Поскольку в каждый прямоугольник можно поставить не более четырех не бьющих друг друга ладей (в первом случае есть только 4 столбца, во втором - 4 строки), то в каждый прямоугольник нужно поставить ровно 4 ладьи, притом, очевидно, количество допустимых расстановок в прямоугольнике 4x5 и 5x4 совпадает.
Считаем количество расстановок в прямоугольнике 4x5. В первую горизонталь можно поставить ладью пятью способами, во вторую четырьмя, в третью тремя, во вторую двумя. Всего способов расставить 4 не бьющие друг друга ладьи в прямоугольник 4x5 оказывается .
Во второй белый прямоугольник можно расставить 4 не бьющие друг друга ладьи тоже 120 способами, расстановки выбираются независимо, так что всего способов расставить ладьи на белые клетки .
2. Чёрные клетки
Аналогично, есть два независимых квадрата 4x4 и 5x5. Тут есть две возможности: на большой квадрат поставить 5 ладей, на маленький 3; на большой 4, на маленький 4.
1) 5 + 3: в большой квадрат ладьи расставляются 5! = 120 способами.
Если в маленьком не ставить ладью на четвёртую горизонталь, будет 4! = 24 способов, а ту горизонталь, на которую будем не ставить ладью, можно выбрать 4 способами. Тогда на маленький квадрат есть расстановок.
Всего для этой возможности есть вариантов.
2) 4 + 4: в маленький квадрат 4! = 24 способа, в большой способов.
Итого здесь вариантов.
Всего способов расставить ладьи на чёрные клетки, таким образом,
Заметим, что это число можно было получить по-другому. 9 ладей можно поставить на эти квадраты способами, а потом, убирая каждую из 9 ладей, получаем те же
вариантов.