Предмет: Математика,
автор: nialls2313
Номер 535 даю 40 баллов.Кто хорошо объяснит отмечу лучшим.
Приложения:
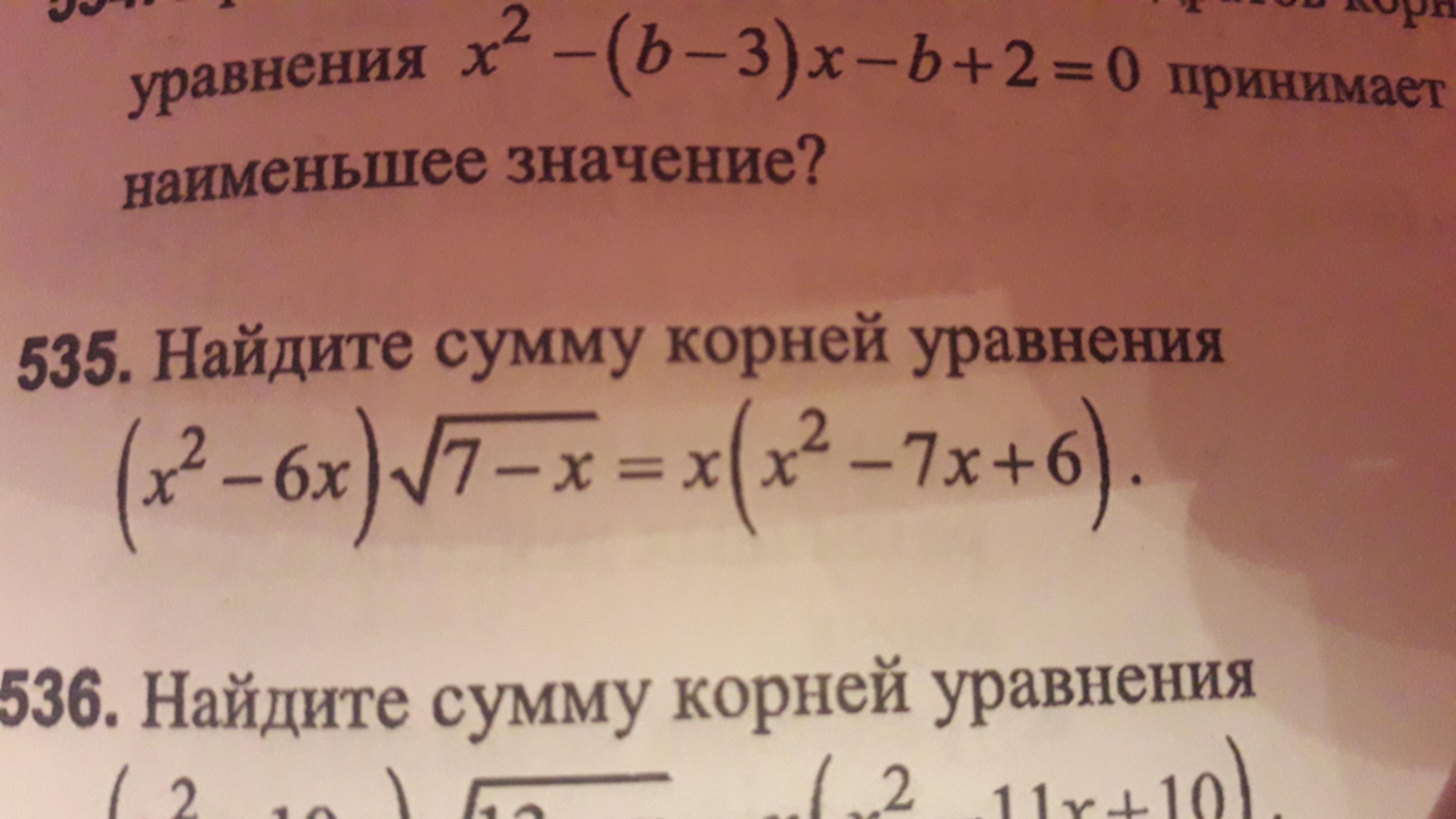
Ответы
Автор ответа:
0
Решение задания приложено
Приложения:

Автор ответа:
0
Ответ:
9
Пошаговое объяснение:
ОДЗ уравнения
разложим на множители квадратный двучлен:
отсюда
у последнего уравнения:
4 ый корень не удовлетворяет ОДЗ
сумма трех корней:
Похожие вопросы
Предмет: Математика,
автор: Terasiner
Предмет: Математика,
автор: juliamaksiyk87
Предмет: Другие предметы,
автор: ermakovaalina331
Предмет: Алгебра,
автор: Nick3232
Предмет: Физика,
автор: M1shutka