Предмет: Геометрия,
автор: anto80344
Сторони трикутника дорівнюють 40 см, 40 см і 48 см. Знайдіть відстані від центра описаного кола до сторін трикутника.
Ответы
Автор ответа:
12
По формуле Герона вычислим площадь треугольника
полупериметр
p = (40 + 40 + 48)/2 = 40 + 24 = 64 см
Площадь
S² = p(p-a)(p-b)(p-c) = 64*(64-40)(64-40)(64-48) = 64*24²*16
S = √(64*24²*16) = 8*24*4 = 768 см
---
Радиус описанной окружности
R = abc/(4S) = 40*40*48 / (4 * 768) = 10 * 40 * 2 / 32 = 5 * 5 = 25 см
---
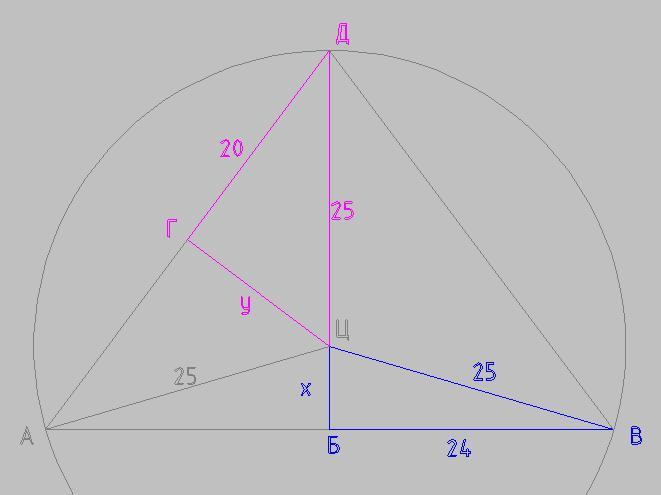
ΔАВЦ - равнобедренный, т.к. две его стороны - это радиусы описанной окружности ΔАВД
ЦБ - высота ΔАВЦ, одновременно и его биссектриса и сторону АВ делит пополам
БВ = АВ/2 = 48/2 = 24 см
По т. Пифагора для синего треугольника
БЦ² + БВ² = ВЦ²
х² + 24² = 25²
x² = 25² - 24² = (25 + 24)(25 - 24) = 49
x = 7 см
---
Аналогично по т. Пифагора для малинового треугольника
у² + 20² = 25²
y² = 25² - 20² = (25 + 20)(25 - 20) = 45*5 = 9*25
y = 3*5 = 15 см
Приложения:
anto80344:
Спасибо огромное!
Похожие вопросы
Предмет: Математика,
автор: sultan25111986
Предмет: Английский язык,
автор: ftr2020
Предмет: Алгебра,
автор: MrBleik
Предмет: Биология,
автор: илий1
Предмет: Право,
автор: Vika20162017