Предмет: Математика,
автор: 2089999999
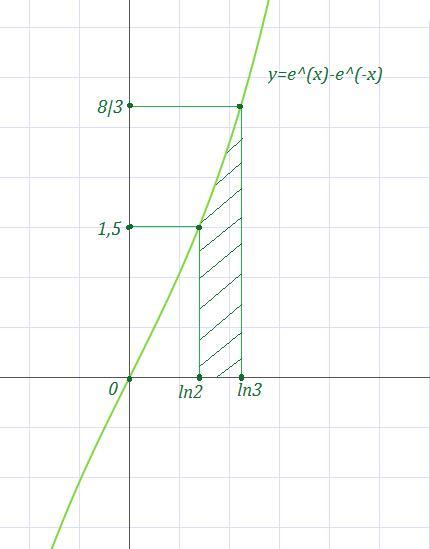
Найдите площадь фигуры, ограниченной линиями y=e^x-e^-x, x=ln 2, x=ln 3,y=0
помогите пожалуйста
Ответы
Автор ответа:
1
Ответ: .
Пошаговое объяснение:
Приложения:
2089999999:
спасибо большое!
Автор ответа:
0
Ответ: во вложении Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Физика,
автор: gordey638109
Предмет: Математика,
автор: mkallxx36
Предмет: География,
автор: plitvinova
Предмет: Математика,
автор: Makcik2016
Предмет: Информатика,
автор: Flasch