Предмет: Алгебра,
автор: Аноним
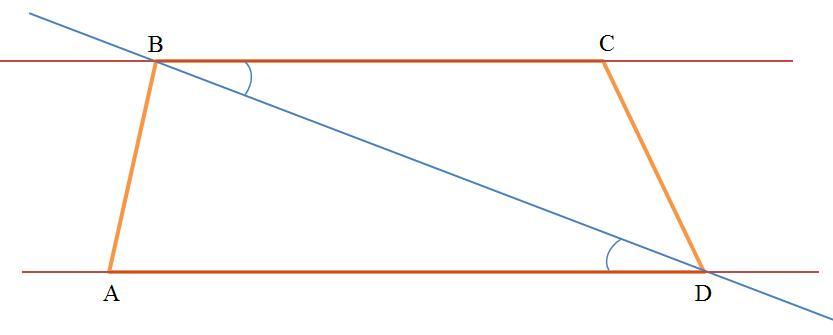
В четырехугольнике ABCD стороны BC и AD параллельны. Докажите, что угол CBD = углу ADB.
Ответы
Автор ответа:
18
Ответ:
Пропустим через точки A и D, B и C, B и D прямые (см. рисунок). Тогда прямые BC и AD параллельны. Тогда как секущая прямая BD образует накрест лежащие углы ∠CBD и ∠ADB. На основе следующей теоремы о параллельных прямых заключаем, что ∠CBD и ∠ADB.
Теорема. Если две параллельные прямые пересечены секущей, то накрест лежащие углы, образованные этими прямыми и секущей, равны.
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: Аноним
Предмет: Математика,
автор: pavelzebrikov9
Предмет: Русский язык,
автор: aarlanov181
Предмет: Математика,
автор: Ольга0411
Предмет: Математика,
автор: NADEZDAK