Предмет: Алгебра,
автор: Stickmaster119
КТО ЗНАЕТ АНГЛИЙСКИЙ СРОЧНО ПОМОГИТЕ РЕШИТЬ!!!
Приложения:

Stickmaster119:
ПОЖАЛУЙСТА :(
условие задачи напиши по-русски ...
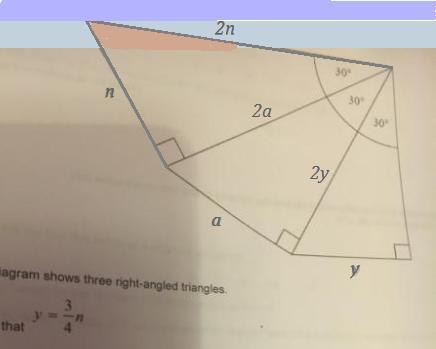
Диаграмма показывает три правоугольных треугольника
докажите что y = 3
_n
4
докажите что y = 3
_n
4
прямоугольных треугольника
право-угольных треугольника
нет
три прямоугольных треугольника(если посмотреть на рисунок)
есть решение гораздо проще, но уже некуда прикрепить))
связано с тем, что 3*30=90
нет, только с тем, что "катет против угла в 30 градусов..." и все... остальное дополнительными построениями (здесь можно построить равносторонний... треугольник 30+30 только))
Ответы
Автор ответа:
1
Ответ:
Катет,лежащий против угла в 30 градусов = половине гипотенузы.
У первого справа треугольника катет = у, а его гипотенуза = 2у.
У второго треугольника обозначим катет, лежащий против угла в 30° , через а, тогда его гипотенуза = 2а, и по теореме Пифагора имеем
У третьего справа треугольника катет = n , гипотенуза = 2n, и по теореме Пифагора имеем
Решение №2, которое дал пользователь LFP, но не имел возможности его записать, приведено во 2-ом вложении.
Приложения:
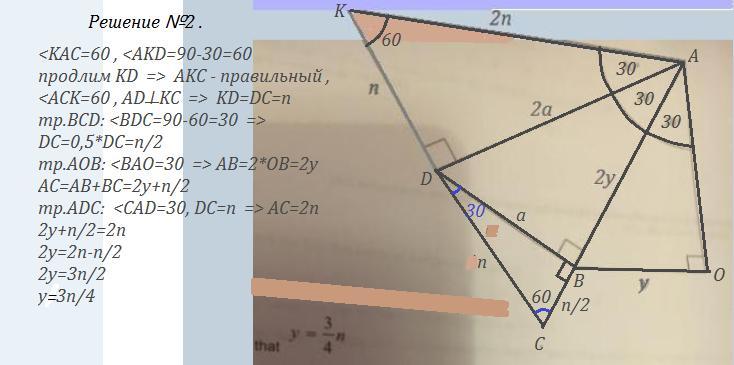
да, и еще сторону n продолжить-- получится еще один прямоугольный треугольник с гипотенузой n и катетом n/2... и 2n=2y+(n/2)
Ясно, спасибо.
С вашего позволения я записала ваше решение , так как вы не смогли его сами записать. А мне оно понравилось. Чтобы не пропало...
и отлично)) спасибо) рада, что понравилось...
Автор ответа:
1
Ответ:
Объяснение:
решение внизу
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: Liza14073
Предмет: Математика,
автор: azhahmetovagulnaz
Предмет: Физика,
автор: artemsaravara41
Предмет: Математика,
автор: Аноним