Предмет: Геометрия,
автор: 738383837
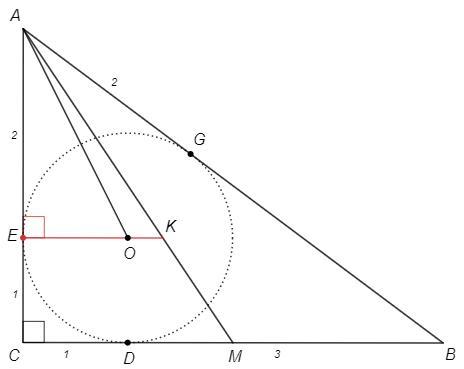
ДАНО: ▲АВС, угол С=90 градусов. Е,D,g- точки касания вписанной окружности со сторонами АС,ВС,АВ. EC=8, Bg=24.
ДОКАЗАТЬ: ОЕ проходит через точку К- точка пересечения медиан.
НАЙТИ: S▲AKO
Simba2017:
СB=32
AC=x+8
AB=x+24
через площадь нашла x=16
тогда стороны треугольника все известны
дальше через подобие доказывая что K на EO
нахожу EK
EO=8
AE=16
ну и через разность площадей треугольников AKE и AOE нахожу нужную площадь
Ответы
Автор ответа:
2
Разделим задачу на 8.
CD=CE=1, BD=BG=3, AE=AG=x (отрезки касательных из одной точки)
(x+1)^2 +4^2 =(x+3)^2 => x=2
AE=2, AC=3
AE/AC =AK/AM =2/3 (медианы делятся точкой пересечения...)
KE||BC (обратная теорема Фалеса)
OE⊥AC (радиус в точку касания) => OE||BC
O и K лежат на перпендикуляре через E.
KE=2/3 MC =2/3 *2 =4/3
OK= KE-OE =4/3 -1 =1/3
S(AKO)= 1/2 OK*AE =1/2 *1/3 *2 =1/3 (см^2)
Результат умножаем на 8^2, ответ: 64/3 (см^2)
Приложения:
Похожие вопросы
Предмет: Биология,
автор: vasuksofia27
Предмет: Физика,
автор: halepakarolina
Предмет: География,
автор: 2000ulianam
Предмет: Биология,
автор: Meeander
Предмет: Математика,
автор: vanek12324